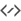Multiquadrícula

Una capa d'emplenament basada en el mètode de multiquadrícula de Bruijn de 1981 per a generar Tessel·lació de Penrose. Aquest generador projecta una quadrícula hiperdimensional en un pla en 2D, donant alguns patrons força interessants. A més de veure's bé, hi ha algunes característiques interessants i potencialment útils que tenen els patrons resultants:

1. Sempre produeix rombes, és a dir, formes de diamant o de rectangle. Això és particularment útil per a artistes del 3D.

2. Per a totes les dimensions excepte per a les 3, 4 i 6 els resultats són aperiòdics, això vol dir que mai es repetirà en l'amplada o alçada de la imatge.

3. Els resultats es repeteixen simètricament al voltant del centre. La quantitat de les repeticions simètriques és la mateixa que la quantitat de les dimensions projectades.

També se sap que els patrons resultants apareixen a la natura com a quasicristalls.

Formes

La carn de l'algoritme. Els valors predeterminats per a això produeixen la tessel·lació de Penrose en estrella.

Dimensions

La quantitat de dimensions que té l'hipergelosia. 3 és una gelosia de cubs, 4 és una gelosia de tesseractis, 5 és una gelosia de penteractis, i així successivament.

Multiquadrícula amb dimensions diferents, començant en 3 i acabant en 12. Les 3D, 4D i 6D estan acolorides amb el factor de color d'intersecció, mentre que la resta utilitza exclusivament la proporció. En el 3D, 4D i 6D, tots els rombes tenen la mateixa proporció.

Divisions

Efectivament un allunyament. Aquestes són les subdivisions de la longitud de l'amplada entre el centre i la cantonada de la imatge. Després s'utilitza per a determinar quantes línies es projectaran per a cada dimensió.

Desplaçament

Controla quant es desplaça cada conjunt de línies des del centre de la imatge. En canviar aquest valor, el patró dins de la mateixa dimensió canviarà significativament.

Multiquadrícula amb 5 dimensions i 20 divisions. Els desplaçaments d'esquerra a dreta són: 0,3, 0,1, 0,2 (tessel·lació de Penrose en estrella), 0,3, 0,4 (tessel·lació de Penrose en Sol), 0,48.

Línies

Amplada de la línia

L'amplada en píxels de la imatge dels contorns dels rombes. A causa de la forma en què es dibuixen els rombes, encara hi ha una línia fina visible a 0 px.

Línies de connexió

De manera opcional, això dibuixa línies entre els diferents costats de la forma. Generalment s'utilitza per a mostrar que una tessel·lació específica té certes regles de coincidència, però també ofereix resultats atractius.

Angle agut

Dibuixa un arc entre els costats que es connecten a un angle agut.

Angle obtús

Dibuixa un arc entre els costats que es connecten a un angle obtús.

Creu

Dibuixa dues línies creuades entre els costats de cada rombe. Particularment interessant amb 0 com a amplada de la línia.

Colors

Imatge que mostra la tessel·lació de Penrose en estrella amb 29 divisions i línies de connexió en els angles aguts. El complex degradat i la combinació de la proporció i l'índex per a donar color a la imatge, donen com a resultat alguns dels resultats més impressionants que es poden obtenir des d'aquesta capa d'emplenament.

Aquesta secció controla tots els colors, tots agrupats perquè els botons de color del Krita permeten arrossegar i deixar anar colors. Podreu canviar el color dels contorns i les línies del connector, i hi ha un degradat per a pintar els rombes de manera individual.

Els factors de color determinen quines propietats de cada rombe s'utilitzaran per a determinar el seu color. Aquest valor s'utilitzarà com un multiplicador, per a finalment donar com a resultat un valor que es pot utilitzar per a obtenir el valor del degradat.

Relació

Pinta els rombes segons la seva proporció. Els rombes prims tenen una proporció baixa, els rombes gruixuts tenen una proporció alta i els quadrats perfectes tenen la proporció més grossa.

Interseca

Pinta els rombes segons les línies que es creuen en aquest rombe. En efecte, això dona color al rombe depenent de quin costat de la hipergelosia es troba el rombe, com queda especialment clar quan s'estableix la dimensió a 3.

Índex

Pinta els rombes segons l'índex de les línies que es creuen des del centre. En efecte, els rombes més propers al centre tindran un valor més baix, mentre que els rombes més allunyats del centre tindran un valor més alt.