Griglia multipla

Un livello di riempimento basato sul metodo a griglia multipla di de Bruijn del 1981 per generare le tassellature di Penrose. Questo generatore proietta un reticolo a griglia iperdimensionale su un piano 2D, fornendo dei motivi molto belli. Oltre ad essere belli, offrono alcune funzionalità interessanti e potenzialmente utili che i modelli risultanti hanno:

1. Produce sempre rombi, cioè rombi o rettangoli. Ciò è particolarmente utile per gli artisti 3D.

2. Per tutte le dimensioni tranne 3, 4 e 6 i risultati sono aperiodici, questo significa che non si ripeterà mai nella larghezza o altezza dell’immagine.

3. I risultati si ripetono simmetricamente attorno al centro. La quantità di ripetizioni simmetriche è uguale alla quantità di dimensioni proiettate.

I motivi risultanti sono noti anche per presentarsi in natura come quasicristalli.

Forme

La carne dell’algoritmo. I valori predefiniti per questo producono la tassellatura a stella di Penrose.

Dimensioni

La quantità di dimensione che ha l’iperreticolo. 3 è un reticolo di cubi, 4 è un reticolo di tesseratti, 5 è un reticolo di penteratti, e così via.

Griglia multipla con dimensioni diverse, partendo con 3 e terminando con 12. 3D, 4D e 6D sono colorati con il fattore di colore intersecato, mentre il resto usa esclusivamente il rapporto. In 3D, 4D e 6D, tutti i rombi hanno lo stesso rapporto.

Regioni

Effettivamente uno zoom indietro. Questa è la suddivisione della lunghezza della larghezza tra il centro e l’angolo dell’immagine. Questo viene quindi utilizzato per determinare quante linee sono proiettate per ciascuna dimensione.

Scostamento

Questo controlla quanto ogni insieme di linee è spostato dal centro dell’immagine. La modifica di questo valore cambia il motivo all’interno della stessa dimensione in modo significativo.

Griglia multipla con 5 dimensioni e 20 divisioni. Gli scostamenti da sinistra a destra sono: 0,3, 0,1, 0,2 (tassellatura a stella di Penrose), 0,3, 0,4 (tassellatura a sole di Penrose), 0.48.

Linee

Spessore delle linee

La larghezza dei contorni dei rombi nei pixel dell’immagine. A causa del modo in cui sono disegnati i rombi, c’è ancora una linea sottile visibile a 0 px.

Linee connettore

Questo opzionalmente traccia delle linee tra i diversi lati della forma. Questo è in genere utilizzato per mostrare che una tassellatura specifica ha determinate regole di corrispondenza, ma fornisce anche risultati interessanti.

Angolo acuto

Traccia un arco tra i lati che si collegano a un angolo acuto.

Angolo ottuso

Traccia un arco tra i lati che si collegano a un angolo ottuso.

Croce

Disegna due linee incrociate tra i lati di ogni rombo. Particolarmente interessante con larghezza di linea 0.

Colori

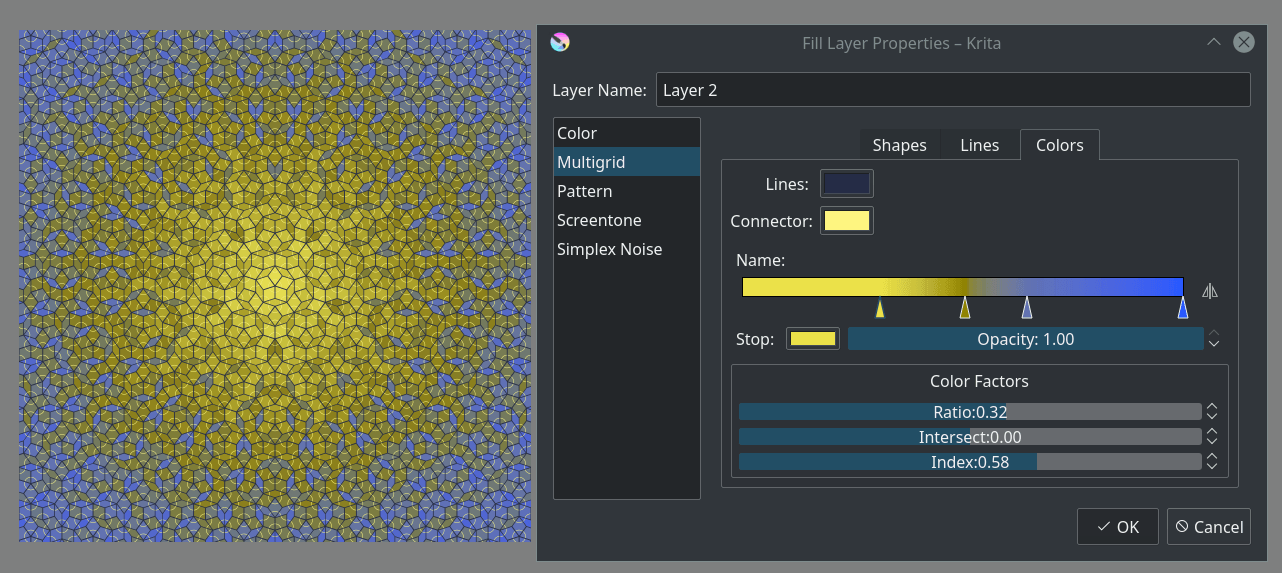
Immagine che mostra la tassellatura a stella di Penrose con 29 divisioni e linee di connessione agli angoli acuti. Il complesso gradiente e la combinazione di rapporto e indice per colorare l’immagine danno luogo ad alcuni dei risultati più impressionanti che si possano ottenere da questo livello di riempimento.

Questa sezione controlla tutti i colori, tutti raggruppati insieme perché i pulsanti dei colori di Krita consentono di trascinare e rilasciare i colori l’uno sull’altro. Puoi cambiare il colore per i contorni e le linee di connessione, e c’è una sfumatura per colorare i singoli rombi.

I fattori di colore determinano quale proprietà di ciascun rombo è utilizzata per determinarne la colorazione. Questo valore viene utilizzato come moltiplicatore, per ottenere infine un valore che può essere utilizzato per ottenere il valore dal gradiente.

Rapporto

Questo colora i rombi in base al loro rapporto. I rombi sottili hanno un rapporto basso, i rombi spessi hanno un rapporto alto e i quadrati perfetti hanno il rapporto più grande.

Interseca

Questo colora i rombi in base a quali linee intersecanti hanno prodotto questo rombo. In effetti, questo colora il rombo a seconda di su quale lato dell’iperreticolo il rombo si trovi, come è particolarmente chiaro quando si imposta la dimensione a 3.

Indice

Questo colora i rombi in base all’indice delle linee intersecanti dal centro. In effetti, i rombi più vicini al centro avranno un valore inferiore, mentre i rombi più lontani dal centro avranno un valore più alto.