Wielosiatka

Warstwa wypełnienia oparta na sposobie wielosiatki Bruijn 1981 do tworzenia Kafelków Penrose . Ten generator rzutuje hiperwymiarową siatkę na płaszczyznę 2d, dając w wyniku ciekawe wzorce. Poza tym, że wygląda to ciekawie, wzorce mają kilka ciekawych i potencjalnie użytecznych możliwości:

1. W wyniku zawsze daje romby, które są w kształcie diamentów lub prostokątów. Jest to szczególnie użyteczne dla artystów 3d.

2. Dla wszystkich wymiarów poza 3, 4 oraz 6 wyniki są aperiodyczne, co oznacza że nie powtórzą się nigdy w szerokości lub wysokości obrazu.

3. Wyniki powtarzają się symetrycznie wokół środka. Liczba symetrycznych powtórzeń jest ta sama, co liczba rzutowanych wymiarów.

Powstające wzorce pojawiają się także w naturze jako kwazikryształy.

Kształty

Mięso algorytmu. Domyślne wartości dają w wyniku kafelki gwiezdne Penrose.

Wymiary

Liczba wymiarów, którą ma hipersiatka. 3 jest siatką sześcianów, 4 jest siatką czterościanów, 5 jest siatką pięciościanów, itd.

Wielosiatka o rożnych wymiarach, rozpoczynająca się na 3 i kończąca na 12. 3d, 4d oraz 6d są kolorowane przy użyciu współczynnika barwy na przecięciu, podczas gdy reszta używa wyłącznie współczynnika udziału. w 3d, 4d oraz 6d, wszystkie romby mają taki sam współczynnik udziału.

Podziały

Właściwie jest to oddalenie widoku. Są to podpodziały długości na szerokości pomiędzy środkiem i narożnikiem obrazu. Jest to następnie używane do określenia liczby linii rzutowanych dla każdego wymiaru.

Odsunięcie

Steruje to tym jak bardzo zestawy linii są odsunięte od środka obrazu. Zmiana tej wartości znacznie zmienia wzorzec o tym samym wymiarze.

Wielosiatka o 5 wymiarach i 20 podziałach. Odsunięcie od lewej do prawej to: 0.3, 0.1, 0.2 (kafelki gwiezdne Penrose), 0.3, 0.4 (kafelki słoneczne Penrose), 0.48.

Linie

Szerokość linii

Szerokość zarysów rombów w pikselach obrazu. Ze względu na sposób rysowania rombów, nadal widać linię o cienkości włosa przy 0 pikselach.

Linie łączące

Opcjonalnie rysuje to linie pomiędzy różnymi stronami kształtu. Zazwyczaj jest to używane do pokazania, że dane kafelkowanie ma pewne zasady dopasowywania, ale daje także ciekawie wyglądające wyniki.

Kąt ostry

Rysuje łuk pomiędzy bokami, który łączy się z kątem ostrym.

Kąt rozwarty

Rysuje łuk pomiędzy bokami, który łączy się z kątem rozwartym.

Krzyżyk

Rysuje dwie linie przecięcie pomiędzy dwoma bokami rombu. Szczególnie ciekawe przy 0 szerokości linii.

Barwy

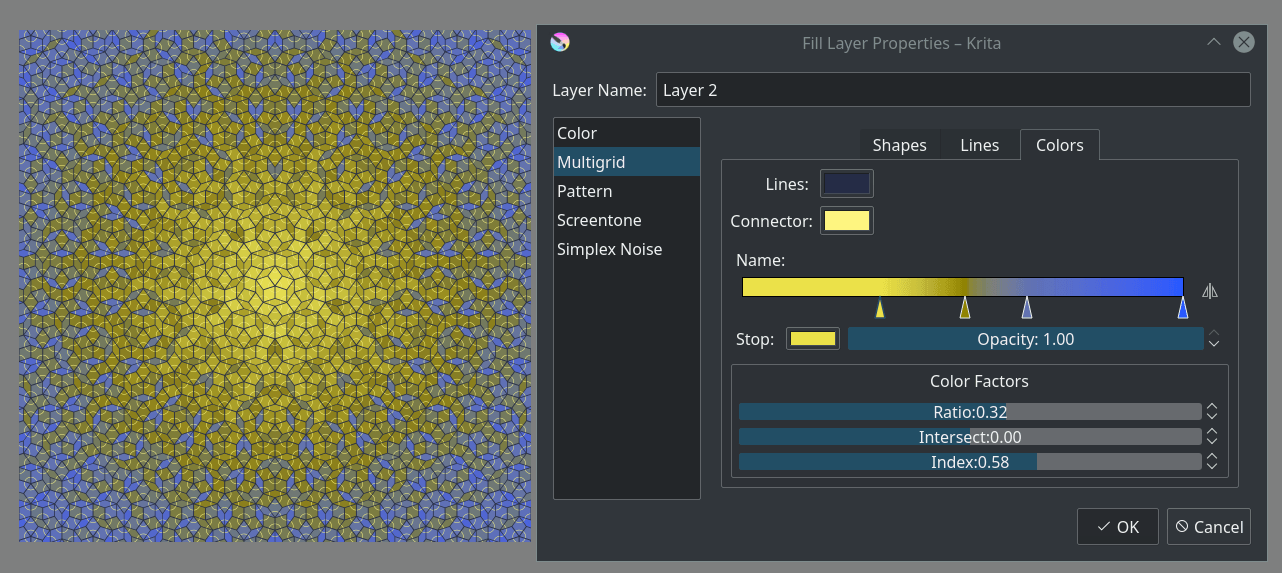
Obraz pokazujący gwiezdne kafelki Penrose z 29-cioma podziałami i liniami łączącymi w miejscu ostrych kątów. Złożony gradient i połączenie współczynnika udziału oraz indeksu do pokolorowania obrazu daje ciekawy wynik, który można uzyskać z tej warstwy wypełnienia.

Ten obszar steruje wszystkimi barwami, wszystkie zgrupowane razem, bo przyciski barw w Kricie umożliwiają upuszczanie na nie barw. Możesz zmienić barwę dla linii zarysu i linii łączących. Istnieje też gradient do pokolorowania osobnych rombów.

Współczynniki barw określają jakie właściwości są używane dla każdego rombu, aby go pokolorować. Wartość ta jest używana jako mnożnik, aby w wyniku uzyskać wartość, której można użyć do uzyskania wartości z gradientu.

Stosunek

To koloruje romby na podstawie ich współczynnika udziału. Cienkie romby, które mają ten współczynnik niski, grube romby mają go wysoki, a doskonałe kwadraty mają go największy.

Przecięcie

To koloruje romby na podstawie przecinających linii w tym rombie. W wyniku, koloruje to romb w zależności od strony hipersiatki, po której znajduje się romb i jest to szczególnie widoczne po ustawieniu wymiaru na 3.

Indeks

Koloruje to romby na podstawie indeksu przecinających linii od środka. W wyniku tego, romby bliżej środka będą miały niższe wartości, podczas gdy romby dalej od środka będą miały wyższe wartości.