Szybki podręcznik SeExpr

Ta strona wyszczególnia wszystkie dostępne zmienne, funkcje oraz operatory w SeExpr. Jest to znacznie pozmieniane wydanie dokumentacji użytkownika, przystosowane do użytku z Kritą.

Zobacz także

• Kod źródłowy w KDE Invent

• Dokumentacja API dla SeExpr od Disney’a

Zobacz także

• Wprowadzenie do SeExpr

• SeExpr

• Skrypty SeExpr

• „Generator proceduralny tekstur (przykład i życzenia)” na Artyści Krity

• Artykuły Inigo Quilez

• Książka jednostek cieniujących

Zmienne

Zewnętrzne zmienne

Te zmienne są dostarczane przez aplikacje gospodarza, w tym przypadku Kritę. Są rejestrowane przy użyciu pomocy przy uzupełnianiu wyrażeń SeExpr, do której dostęp można uzyskać poprzez Ctrl+Spacja.

$u, $v

Położenie piksela we współrzędnych znormalizowanych.

$w, $h

Szerokość i wysokość obrazu w pikselach.

Zmienne lokalne

Lokalne zmienne można określić na początku wyrażenia:

$a=noise($P);
$b=noise($a * 1);
pow($a, 0.5) + $b

Zewnętrzne zmienne także można zastąpić miejscowymi przypisaniami. Może okazać się to użyteczne, aby przeskalować np. skalę szumu:

$P=$P * 10; # zwiększ częstotliwość szumu
fbm(vnoise($P) + $P/4)

Możesz także określić zmienne w przestrzeni nazw np.:

$A::a = $u * 10;

Struktury sterujące

SeExpr dostarcz dobrze znanej struktury warunkowej if:

if ($ u > 0.5) {
    $color = [0, 0, 1];
}
else {
    $color = [1, 0, 0];
}

$color

Oraz trójstronny operator:

$u=$i < .5 ? 0.0 : 10.0

Możesz dowolnie zagnieżdżać trójstronne operatory, np.:

$color = $u < .5 ? ($v < 0.5 ? [0, 0, 1] : [1, 0, 0]) : [0, 1, 0];
$color

Możesz uzyskać to amo przy użyciu struktur if:

if ($ u > 0.5) {
    if ($v < 0.5) {
        $color = [0, 0, 1];
    }
    else {
        $color = [1, 0, 0];
    }
}
else {
    $color = [1, 0, 0];
}

$color

Operatory (wyszczególnione w kolejności malejącej)

[a,b,c]

konstruktor wektora

$P[ n ]

dostęp do składowej wektora

Podpowiedź

n musi być 0, 1 lub 2, np.:

$P[0]

^

potęgowanie

Informacja

To samo co funkcja pow.

!

logiczne NIE

~

odwrócenie

Podpowiedź

~$A

daje ten sam wynik co:

1 - $A

*/ %

mnożenie, dzielenie, moduł

Informacja

% jest tym samym czym funkcja fmod.

+-

dodaj, odejmij

<> <= >=

porównanie: mniejsze niż, większe niż, mniejsze lub równe, większe lub równe

Informacja

Używa tylko pierwszej składowej wektora.

== !=

równość, nierówność

&&

logiczne TAK

||

Logiczne LUB

?:

trójstronny operator if

Podpowiedź

Przykład:

$u < .5 ? 0 : 1

->

apply - Funkcja po prawej od strzałki jest stosowana do wyrażenia po lewej.

Podpowiedź

Przykłady:

$Cs->contrast(.7) -> clamp(0.2,0.8)
$u->hsi(20,1.2,1,$Cs->gamma(1.2))

Operatory przypisania

Poza podstawowym poleceniem przypisania:

$foo=$bar

przypisanie operatorem możesz także wykonać w ten sposób:

$foo += $bar;

co jest równoważne:

$foo=$foo + $bar;

Dodatkowo, jest tutaj:

• +=

• -=

• /=

• %=

• *=

• ^=

Uwagi

Możesz dodawać uwagi do swojego skryptu po wstawieniu znaku #. SeExpr pominie wtedy dalszą część wiersza przy wyświetlaniu. Nie są one jednak pomijane; uwag nadal można użyć do określenia prawidłowych zakresów wartości liczb całkowitych, rzeczywistych oraz zmiennych wektorowych. Spowoduje to, że będziesz w stanie zarządzać nimi przy użyciu elementów interfejsu, które będą przyjmować dany zakres.

Podpowiedź

$var0 jest zmienną w postaci liczby całkowitej z zakresu od 0 do 10 włącznie:

$var0=0; # 0, 10

$var1 jest zmienną rzeczywistą o tym samym zakresie:

$var1=0; # 0.000, 10.000

$var2 jest zmienną wektorową:

$var2=[0, 0, 0] # 0.000, 10.000

To późniejsze jest bardzo pomocne; SeExpr odbiera wektory z zakresu [0, 1] jako barwy:

# to jest ciemny czerwony
$color=[0.5, 0, 0] # 0.000, 1.000

We wszystkich przypadkach, jeśli nie określono, przypisany zakres elementu interfejsu będzie się wahał od 0 do 1.

W wielowierszowych wyrażeniach, do każdego wiersza można dodać osobną uwagę.

Funkcje logarytmiczne

float printf ( string format, [param0, param1, …] )

Wyświetla ciąg znaków na standardowe wyjście z danym formatowaniem. Możliwe są parametry formatowania %f dla liczby rzeczywistej (bierze pierwszą składową argumentu wektora) lub %v dla wektora.

Podpowiedź

Na przykład, jeśli napiszesz:

$u = printf("test %f %v",[1,2,3],[4,5,6]);

dostałbyś w swojej konsoli:

test 1 [4,5,6]

string sprintf ( string format, [double|string, double|string, …] )

Zwraca ciąg znaków sformatowanych danym wartościami. Po więcej szczegółów, zobacz man sprintf.

Funkcje barwy, masek oraz ponownego mapowania

float bias ( float x, float b)

Zmienność gammy, gdzie parametr sterujący zmienia się od 0 do 1 z wartościami > 0.5 ciągnącymi krzywą w górę oraz wartościami < 0.5 ciągnącymi krzywą w dół. Określone jako pow(x, log(b)/log(0.5)).

float boxstep ( float x, float a )

float gaussstep ( float x, float a, float b )

float linearstep ( float x, float a, float b )

float smoothstep ( float x, float a, float b )

Funkcje krokowe są równe zero dla x < a oraz dla x > b (lub x > a w przypadku kroku jako pudełko). Pomiędzy a oraz b, wartość zmienia się w sposób ciągły od zera do jednego. Funkcja gausstep używa standardowej krzywej „dzwona”, która opiera się na krzywej wykładniczej. Funkcja smoothstep używa krzywej sześciennej. Intuicyjnie, gausstep ma ostrzejsze przejście w pobliżu jednego końca i bardziej miękkie przejście w pobliżu zera, podczas gdy smoothstep ma średnią miękkość w pobliżu jedynki oraz zera.

float clamp ( float x, float lo, float hi )

Zwiąż x z zakresem [lo, hi].

float compress ( float x, float lo, float hi )

Ściąga zakres dynamiczny z wartości [0, 1] do [lo, hi].

float contrast ( float x, float c )

Dostosuje kontrast. Dla c od 0 do 0.5, kontrast jest zmniejszany. Dla c > 0.5, kontrast jest zwiększany.

float expand ( float x, float lo, float hi )

Rozciąga zakres dynamiczny z wartości [lo, hi] do [0, 1].

float fit ( float x, float a1, float b1, float a2, float b2 )

Linowe mapowanie ponowne [a1..x..b1] to [a2..x..b2]

float gamma ( float x, float g)

pow(x, 1/g)

float invert ( float x )

Odwróć wartość. Określone jako 1 - x.

color hsi ( color x, float h, float s, float i, float map=1 )

Funkcja hsi przesuwa odcień o h (w stopniach) i skaluje nasycenie oraz natężenie o s oraz i odpowiednio. Można dostarczyć mapę do sterowania przesunięciem - pełne przesunięcie nastąpi, gdy mapa jest równa jeden i nie nastąpi w ogóle, gdy mapa jest równa zero. Przesunięcie będzie skalowane pomiędzy wartością zero oraz jeden.

color hsltorgb ( color hsl )

color rgbtohsl ( color rgb )

Przekształcenia barwa RGB na HSL. HSL to Hue (z ang. odcień), Saturation (z ang. nasycenie), Lightness (z ang. światłość) (wszystkie w zakresie``[0, 1]``). Te funkcje zostały również rozszerzone o wsparcie dla wartości RGB oraz HSL spoza zakresu [0, 1] w sensowy sposób. Dla każdej wartości RGB czy HSL (poza wartościami ujemnymi) przekształcenia są jednoznacznie określone i odwracalne.

color midhsi ( color x, float h, float s, float i, float map, float falloff=1, int interp=0 )

Funkcja midhsi jest taka jak funkcja hsi z takim wyjątkiem, że mapa sterująca znajduje się wokół punktu środkowego (wartość 0.5) i może skalować przesunięcie w obu kierunkach. W punkcie środkowym, nie następuje żadne przesunięcie. W punkcie 1.0 następuje pełne przesunięcie, a w punkcie 0.0 pełne odwrotne przesunięcie. Dostępne są dodatkowe elementy sterujące falloff oraz interp aby dostosować mapę przy użyciu funkcji remap. Domyślnie wartości falloff oraz interp dają brak ponownego mapowania.

float mix ( float a, float b, float alpha )

Przeniknij od a do b wg alfy. Określone jako a*(1-alpha) +b*alpha.

float remap ( float x, float source, float range, float falloff, int interp )

Ogólna funkcja ponownego mapowania. Gdy x jest wewnątrz ± range źródła, to wynik jest równy jeden. Wynik spada do zero poza zakresem do wartości poniżej odległości falloff. Kształt spadku jest sterowany przez interp.

Informacja

Można używać wartości numerycznych oraz nazwanych stałych:

• int linear = 0

• int smooth = 1

• int gaussian = 2

Funkcje szumu

float cellnoise ( vector v )

float cellnoise1 ( float x )

float cellnoise2 ( float x, float y )

float cellnoise3 ( float x, float y, float z )

color ccellnoise ( vector v )

cellnoise tworzy pole sześcianów o stałej barwie na podstawie położenia liczb całkowitych. Jest to to samo co funkcja szumu komórkowego PRMan.

Informacja

ccellnoise daje barwny szum komórkowy.

float fbm ( vector v, int octaves=6, float lacunarity=2, float gain=0.5 )

color cfbm ( vector v, int octaves=6, float lacunarity=2, float gain=0.5 )

vector vfbm ( vector v, int octaves=6, float lacunarity=2, float gain=0.5 )

float fbm4 ( vector v, float time, int octaves=6, float lacunarity=2, float gain=0.5 )

color cfbm4 ( vector v, float time, int octaves=6, float lacunarity=2, float gain=0.5 )

vector vfbm4 ( vector v, float time, int octaves=6, float lacunarity=2, float gain=0.5 )

fbm (Fractal Brownian Motion, z ang. Fraktalne Ruchy Browna) jest wieloczęstotliwościową funkcją szumu. Podstawowa częstotliwość jest taka sama jak funkcja noise. Całkowita liczba częstotliwości sterowanych przez octaves. lacunarity jest odstępem pomiędzy częstotliwościami - wartość 2 oznacza, że każda oktawa jest dwa razy większa od poprzedniej częstotliwości. gain steruje tym, o ile każda częstotliwość jest przeskalowana względem poprzedniej częstotliwości.

Informacja

cfbm oraz cfbm4 daje barwny szum.

vfbm and vfbm4 daje szum wektorowy.

float hash ( float seed1, [float seed2, …] )

Tak jak rand lecz bez wewnętrznych ziaren losowości. Można podać dowolną liczbę ziaren losowości, a wynikiem będzie losowa funkcja na podstawie wszystkich ziaren losowości.

float noise ( vector v )

float noise ( float x, float y )

float noise ( float x, float y, float z )

float noise ( float x, float y, float z, float w )

color cnoise ( vector v)

color cnoise4 ( vector v, float t)

float pnoise ( vector v, vector period )

float snoise ( vector v)

float snoise4 ( vector v, float t)

vector vnoise (vector v )

vector vnoise4 (vector v, float t )

noise jest funkcją losowości, która gładko przechodzi pomiędzy próbkami w miejscach liczb całkowitych. Jest to pierwotna funkcja szumu Ken Perlin.

Informacja

cnoise oraz cnoise4 dają barwny szum.

noise4 daje szum wektorowy ze znakiem.

pnoise daje szum okresowy.

snoise oraz snoise4 daje szum ze znakiem z zakresu [-1, 1].

vnoise daje szum wektorowy ze znakiem.

float rand ( [float min, float max], [float seed] )

Losowa liczba pomiędzy [min, max] (lub [0, 1] jeśli nie określono). Jeśli podano ziarno losowości, to zostanie ono wykorzystane jako dodatkowe do wewnętrznych ziaren losowości i może być użyte do stworzenia wielu odmiennych generatorów.

float turbulence ( vector v, int octaves=6, float lacunarity=2, float gain=0.5 )

color cturbulence ( vector v, int octaves=6, float lacunarity=2, float gain=0.5 )

vector vturbulence ( vector v, int octaves=6, float lacunarity=2, float gain=0.5 )

turbulence jest odmianą fbm gdzie brana jest wartość bezwzględna każdego wyrażenia. Daje to bardziej kłębiasty wygląd.

float voronoi ( vector v, int type=1, float jitter=0.5, float fbmScale=0, int fbmOctaves=4, float fbmLacunarity=2, float fbmGain=0.5)

color cvoronoi ( vector v, int type=1, float jitter=0.5, float fbmScale=0, int fbmOctaves=4, float fbmLacunarity=2, float fbmGain=0.5)

vector pvoronoi ( vector v, float jitter=0.5, float fbmScale=0, int fbmOctaves=4, float fbmLacunarity=2, float fbmGain=0.5)

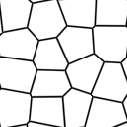
voronoi jest komórkowym wzorcem szumu. Jest to postrzępiona odmiana cellnoise. Parametr rodzaju opisuje różne odmiany funkcji szumu. Parametr jitter steruje tym jak nieregularny jest wzorzec (0 jest zwykłym szumem komórkowym). Parametrów fbm... można użyć do odkształcenia pola szumu. Gdy fbmScale jest równe zero (domyślne), to nie ma odkształceń. Pozostałe parametry są takie same jak dla funkcji fbm.

Podpowiedź

Typy Voronoi od 1 do 5:

Informacja

cvoronoi zwraca losową barwę dla każdej komórki, a pvoronoi zwraca położenie punktu środkowego komórki.

Funkcje zaznaczania

float choose ( float index, float choice1, float choice2, […] )

Wybiera jeden z możliwych wyborów na podstawie indeksu (zakłada się, że z zakresu [0, 1]).

int cycle ( int index, int loRange, int hiRange )

Krąży pomiędzy wartościami spomiędzy zakresu loRange oraz hiRange na podstawie podanego indeksu. Jest to funkcja przesunięcia mod. Wynik jest obliczony jako loRange + wartość % (hiRange-loRange+1).

int pick ( float index, int loRange, int hiRange, [ float weights, … ] )

Wybiera wartości losowo spomiędzy loRange oraz hiRange na podstawie podanego indeksu (dla których jest obliczany hasz). Wartości zostaną rozłożone wg podanych wag. Gdy wartość wagi jest niepodana, to przyjmuje się 1.0.

float wchoose ( float index, float choice1, float weight1, float choice2, float weight2, […] )

Wybiera jeden z możliwych wyborów na podstawie indeksu (zakłada się, że z zakresu [0, 1]). Wartości zostaną rozłożone wg podanych wag.

Podpowiedź

Ten przykład zwraca liczby całkowite z zakresu od 1 do 10:

pick(value, 1, 10)

Ten przykład zwraca wartości 1 oraz 2 dwukrotnie oraz 2,5 raza tak często odpowiednio w porównaniu do innych wartości (3-10):

pick(value, 1, 10, 2, 2.5)

Ten przykład zwraca 10, 11 oraz 13 aż do 20 (12 jest pomijane ze względu na zerową wagę):

pick(value, 10, 20, 1, 1, 0)

Ogólne stałe i funkcje matematyczne

float PI

float PI=3.14159...

float E

float E=2.71828...

float abs ( float x)

Wartość bezwzględna z x.

float cbrt ( float x )

Pierwiastek sześcienny.

float ceil ( float x )

Następna wyższa liczba całkowita.

float exp ( float x )

E podniesione do potęgi x.

float floor ( float x )

Następna niższa liczba całkowita.

float fmod ( float x, float y )

Reszta z x / y.

Informacja

Dostępne również jako operator %.

float log ( float x )

Logarytm naturalny.

float log10 ( float x )

Logarytm dziesiętny.

float max ( float a, float b )

Większy niż a oraz b.

float min ( float a, float b )

Mniejsze z a oraz b.

float pow ( float x, float y )

x do potęgi y.

Informacja

Dostępne również jako operator ^.

float round ( float x )

Najbliższa liczba całkowita.

float sqrt ( float x )

Pierwiastek kwadratowy.

float trunc ( float x )

Najbliższa liczba całkowita w stronę zera.

Funkcje trygonometryczne

float acos ( float x )

Arkus kosinus.

float acosd ( float x )

Arkus kosinus w stopniach.

float acosh ( float x )

Hiperboliczny arcus kosinus.

float asin ( float x )

Arcus sinus.

float asind ( float x )

Arkus sinus w stopniach.

float asinh ( float x )

Hiperboliczny arkus sinus.

float atan ( float x )

Arkus tangens.

float atand ( float x )

Arkus tangens w stopniach.

float atan2 ( float y, float x)

Arkus tangens z wyrażenia y/x pomiędzy -PI i PI.

float atan2d ( float y, float x )

Arkus tangens w stopniach z wyrażenia y/x pomiędzy -180º i 180º.

float atanh ( float x )

Hiperboliczny arcus tangens.

float cos ( float x )

Kosinus.

float cosd ( float x )

Kosinus w stopniach.

float cosh ( float x )

Kosinus hiperboliczny.

float deg ( float x )

Radiany na stopnie.

float hypot ( float x, float y )

Długość wektora 2D [x, y].

float rad ( float x )

Stopnie na radiany.

float sin ( float x )

Sinus.

float sind ( float x )

Sinus w stopniach.

float sinh ( float x )

Sinus hiperboliczny.

float tan ( float x )

Tangens.

float tand ( float x )

Tangens w stopniach.

float tanh ( float x )

Tangens hiperboliczny.

Funkcje wektorowe

float angle ( vector a, vector b )

Kąt pomiędzy dwoma wektorami (w radianach).

vector cross ( vector a, vector b )

Iloczyn wektorowy wektora.

float dist ( vector a, vector b )

Odległość pomiędzy dwoma punktami.

float dot ( vector a, vector b)

Iloczyn skalarny wektora.

float length ( vector v )

Długość wektora.

vector norm ( vector v )

Wektor przeskalowany do długości jednostkowej.

vector ortho ( vector a, vector b )

Wektor prostopadły do dwóch wektorów.

vector rotate ( vector v, vector axis, float angle )

Obraca v wokół osi o dany angle (w radianach).

vector up ( vector v, vector up )

Obraz v tak że punkty na osi Y są zwrócone ku górze.

Obsługa wektorów

Wektory (punkty, barwy oraz wektory 3D) można wymieszać ze skalarami (proste wartości rzeczywiste). Jeśli skalar jest używany w kontekście wektora, to jest on powielony do trzech składowych, tj. 0.5 staje się [0.5, 0.5, 0.5].

Jeśli wektor jest używany w kontekście skalarów, to tylko pierwszy składnik jest używany. Jedną z zalet tego jest to, że wszystkie funkcje, które są przeznaczone do pracy ze skalarami, są od razu rozszerzone na wektory. Na przykład, pick, choose, cycle, spline, itp., będzie działać dobrze na wektorach.

Operatory arytmetyczne takie jak +, *, itp. oraz funkcje skalarne są stosowane na wektorach w sposób wg składowych. Na przykład, zastosowanie funkcji gamma do mapowania, dostosowuje gammę wszystkich trzech kanałów barw.

Funkcje krzywych

Interpolacja wartości parametrów do zestawu punktów sterujących odbywa się poprzez następujące funkcje.

color ccurve ( float param, float pos0, color val0, int interp0, float pos1, color val1, int interp1, […] )

Interpoluje rampę barw określoną przez punkty sterujące w param. Punkty sterujące są określone przez trójki parametrów pos_i, val_i oraz interp_i.

Podpowiedź

Kody interpolacji to:

• 0 - brak

• 1 - liniowy

• 2 - wygładzony

• 3 - po krzywej sklejanej

• 4 - monotoniczna (nieoscylująca) krzywa sklejana

float curve ( float param, float pos0, float val0, int interp0, float pos1, float val1, int interp1, […] )

Interpoluje rampę 1D określoną przez punkty sterujące w param. Punkty sterujące są określone przez trójki parametrów pos_i, val_i oraz interp_i.

Podpowiedź

Kody interpolacji to:

• 0 - brak

• 1 - liniowy

• 2 - wygładzony

• 3 - po krzywej sklejanej

• 4 - monotoniczna (nieoscylująca) krzywa sklejana

float spline ( float param, float y1, float y2, float y3, float y4, […] )

Interpoluje zestaw wartości do danego parametru, gdzie y1, …, yn są rozłożone równo w zakresie [0, 1].

Własne wtyczki

Własne funkcje mogą być napisane w C++ i wczytane jako jeden lub więcej dynamicznych wtyczek. Po więcej szczegółów zajrzyj do Pisanie wtyczek z własnymi wyrażeniami.

Ostrzeżenie

Ta funkcjonalność nie jest dostępna w Kricie.