SeExpr クイックガイド

このページでは SeExpr で利用可能な演算子、関数、変数のすべてを網羅しています。公式の ユーザドキュメント を Krita で使えるように大幅に編集しました。

参考

参考

変数

外部変数

これらの変数はホストアプリケーション、この場合は Krita によって提供されます。Ctrl+Space から使える、SeExpr のオートコンプリート補助が登録されています。

$u, $v

ノーマライズされたピクセル座標。

$w, $h

ピクセルでの画像の幅と高さ。

ローカル変数

ローカル変数は式の初めで定義できます:

$a = noise($P);
$b = noise($a * 1);
pow($a, 0.5) + $b

外部変数はまたローカル割り当てでオーバーライドできます。これはインスタンスのノイズ周波数をスケールするのに便利です:

$P = $P * 10; # increase noise frequency
fbm(vnoise($P) + $P/4)

名前空間付きの変数も定義できます、例えば:

$A::a = $u * 10;

制御構造

SeExpr はよく知られた if 条件分岐を提供しています:

if ($ u > 0.5) {
    $color = [0, 0, 1];
}
else {
    $color = [1, 0, 0];
}

$color

それから 三項演算子 も:

$u = $i < .5 ? 0.0 : 10.0

三項演算子は自由に入れ子にできます、例えば:

$color = $u < .5 ? ($v < 0.5 ? [0, 0, 1] : [1, 0, 0]) : [0, 1, 0];
$color

また同じことが if 条件分岐でもできます:

if ($ u > 0.5) {
    if ($v < 0.5) {
        $color = [0, 0, 1];
    }
    else {
        $color = [1, 0, 0];
    }
}
else {
    $color = [1, 0, 0];
}

$color

演算子 (優先順位の高い方から)

[a,b,c]

ベクトルコンストラクタ

$P[ n ]

ベクトル要素へのアクセス

ヒント

n は0，1や2でなければならず、例えば:

$P[0]
^

べき乗

注釈

pow 関数と同じ。

!

論理否定

~

反転

ヒント

~$A

結果は次と同じ:

1 - $A
*/ %

乗算、除算、余り

注釈

% は fmod 関数と同じ。

+-

加算、減算

<> <= >=

比較: 未満、より多い、以下、以上

注釈

Only uses the first component of a vector.

== !=

等、不等

&&

論理積

||

論理和

?:

if 三項演算子

ヒント

例:

$u < .5 ? 0 : 1
->

apply - The function on the right of the arrow is applied to the expression on the left.

ヒント

例:

$Cs->contrast(.7) -> clamp(0.2,0.8)
$u->hsi(20,1.2,1,$Cs->gamma(1.2))

代入演算子

基本の代入演算ステートメントに加えて:

$foo = $bar

次のような代入演算もできる:

$foo += $bar;

次に等しい:

$foo = $foo + $bar;

さらに他にも:

  • +=

  • -=

  • /=

  • %=

  • *=

  • ^=

コメント

スクリプトには # 文字を使うことでコメントを追加できます。SeExpr はレンダリング時にその行の以降をスキップします。しかし、無視されるわけではありません; コメントは有効な整数、浮動小数とベクトル変数を宣言することができます。これはウィジェットを使って特定の範囲を受け入れることが可能です。

ヒント

$var0 は0から10までの範囲とした整数(integer)変数:

$var0 = 0; # 0, 10

$var1 は同じ範囲の浮動小数(floating point)変数:

$var1 = 0; # 0.000, 10.000

$var2 はベクトル変数:

$var2 = [0, 0, 0] # 0.000, 10.000

後者はとても便利です: SeExpr はベクトルを範囲 [0, 1] の色と見なします:

# this is a dark red
$color = [0.5, 0, 0] # 0.000, 1.000

In all cases, if not specified, the associated widgets' range will go from 0 to 1.

複数列にわたる式では、それぞれの列でコメントすることができます。

ログ関数

float printf ( string format, [param0, param1, ...] )

Prints a string to stdout that is formatted as given. Formatting parameters possible are %f for float (takes the first component of vector argument) or %v for vector.

ヒント

例えば、次のように書くと:

$u = printf("test %f %v",[1,2,3],[4,5,6]);

コンソールにこのように得られます:

test 1 [4,5,6]
string sprintf ( string format, [double|string, double|string, ...] )

Returns a string formatted from the given values. See man sprintf for format details.

色、マスク、リマップ関数

float bias ( float x, float b)

Variation of gamma where control parameter goes from 0 to 1 with values > 0.5 pulling the curve up and values < 0.5 pulling the curve down. Defined as pow(x, log(b)/log(0.5)).

float boxstep ( float x, float a )
float gaussstep ( float x, float a, float b )
float linearstep ( float x, float a, float b )
float smoothstep ( float x, float a, float b )

The step functions are zero for x < a and one for x > b (or x > a in the case of boxstep). Between a and b, the value changes continuously between zero and one. The gausstep function uses the standard Gaussian "bell" curve which is based on an exponential curve. The smoothstep function uses a cubic curve. Intuitively, gausstep has a sharper transition near one and a softer transition near zero whereas smoothstep has a medium softness near both one and zero.

float clamp ( float x, float lo, float hi )

Constrain x to range [lo, hi].

float compress ( float x, float lo, float hi )

Compress the dynamic range from [0, 1] to [lo, hi].

float contrast ( float x, float c )

Adjust the contrast. For c from 0 to 0.5, the contrast is decreased. For c > 0.5, the contrast is increased.

float expand ( float x, float lo, float hi )

Expand the dynamic range from [lo, hi] to [0, 1].

float fit ( float x, float a1, float b1, float a2, float b2 )

Linear remapping of [a1..x..b1] to [a2..x..b2]

float gamma ( float x, float g)

pow(x, 1/g)

float invert ( float x )

Invert the value. Defined as 1 - x.

color hsi ( color x, float h, float s, float i, float map=1 )

The hsi function shifts the hue by h (in degrees) and scales the saturation and intensity by s and i respectively. A map may be supplied which will control the shift - the full shift will happen when the map is one and no shift will happen when the map is zero. The shift will be scaled back for values between zero and one.

color hsltorgb ( color hsl )
color rgbtohsl ( color rgb )

RGB to HSL color space conversion. HSL is Hue, Saturation, Lightness (all in the range [0, 1]). These functions have also been extended to support RGB and HSL values outside of the range [0, 1] in a reasonable way. For any RGB or HSL value (except for negative values), the conversion is well-defined and reversible.

color midhsi ( color x, float h, float s, float i, float map, float falloff=1, int interp=0 )

The midhsi function is just like the hsi function except that the control map is centered around the mid point (value of 0.5) and can scale the shift in both directions. At the mid point, no shift happens. At 1.0, the full shift happens, and at 0.0, the full inverse shift happens. Additional falloff and interp controls are provided to adjust the map using the remap function. The default falloff and interp values result in no remapping.

float mix ( float a, float b, float alpha )

Blend of a and b according to alpha. Defined as a*(1-alpha) +b*alpha.

float remap ( float x, float source, float range, float falloff, int interp )

General remapping function. When x is within ± range of source, the result is one. The result falls to zero beyond that range over falloff distance. The falloff shape is controlled by interp.

注釈

Numeric values or named constants may be used:

  • int linear = 0

  • int smooth = 1

  • int gaussian = 2

ノイズ関数

float cellnoise ( vector v )
float cellnoise1 ( float x )
float cellnoise2 ( float x, float y )
float cellnoise3 ( float x, float y, float z )
color ccellnoise ( vector v )

cellnoise generates a field of constant colored cubes based on the integer location. This is the same as the PRMan cellnoise function.

注釈

ccellnoise outputs color cellnoise.

float fbm ( vector v, int octaves=6, float lacunarity=2, float gain=0.5 )
color cfbm ( vector v, int octaves=6, float lacunarity=2, float gain=0.5 )
vector vfbm ( vector v, int octaves=6, float lacunarity=2, float gain=0.5 )
float fbm4 ( vector v, float time, int octaves=6, float lacunarity=2, float gain=0.5 )
color cfbm4 ( vector v, float time, int octaves=6, float lacunarity=2, float gain=0.5 )
vector vfbm4 ( vector v, float time, int octaves=6, float lacunarity=2, float gain=0.5 )

fbm (Fractal Brownian Motion) is a multi-frequency noise function. The base frequency is the same as the noise function. The total number of frequencies is controlled by octaves. The lacunarity is the spacing between the frequencies - a value of 2 means each octave is twice the previous frequency. The gain controls how much each frequency is scaled relative to the previous frequency.

注釈

cfbm and cfbm4 outputs color noise.

vfbm and vfbm4 outputs vector noise.

float hash ( float seed1, [float seed2, ...] )

Like rand, but with no internal seeds. Any number of seeds may be given and the result will be a random function based on all the seeds.

float noise ( vector v )
float noise ( float x, float y )
float noise ( float x, float y, float z )
float noise ( float x, float y, float z, float w )
color cnoise ( vector v)
color cnoise4 ( vector v, float t)
float pnoise ( vector v, vector period )
float snoise ( vector v)
float snoise4 ( vector v, float t)
vector vnoise (vector v )
vector vnoise4 (vector v, float t )

noise is a random function that smoothly blends between samples at integer locations. This is Ken Perlin's original noise function.

注釈

cnoise and cnoise4 output color noise.

noise4 outputs signed vector noise.

pnoise outputs periodic noise.

snoise and snoise4 output signed noise with range [-1, 1].

vnoise outputs signed vector noise.

float rand ( [float min, float max], [float seed] )

Random number between [min, max] (or [0, 1] if unspecified). If a seed is supplied, it will be used in addition to the internal seeds and may be used to create multiple distinct generators.

float turbulence ( vector v, int octaves=6, float lacunarity=2, float gain=0.5 )
color cturbulence ( vector v, int octaves=6, float lacunarity=2, float gain=0.5 )
vector vturbulence ( vector v, int octaves=6, float lacunarity=2, float gain=0.5 )

turbulence is a variant of fbm where the absolute value of each noise term is taken. This gives a more billowy appearance.

float voronoi ( vector v, int type=1, float jitter=0.5, float fbmScale=0, int fbmOctaves=4, float fbmLacunarity=2, float fbmGain=0.5)
color cvoronoi ( vector v, int type=1, float jitter=0.5, float fbmScale=0, int fbmOctaves=4, float fbmLacunarity=2, float fbmGain=0.5)
vector pvoronoi ( vector v, float jitter=0.5, float fbmScale=0, int fbmOctaves=4, float fbmLacunarity=2, float fbmGain=0.5)

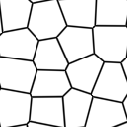
voronoi is a cellular noise pattern. It is a jittered variant of cellnoise. The type parameter describes different variants of the noise function. The jitter param controls how irregular the pattern is (0 is like ordinary cellnoise). The fbm... params can be used to distort the noise field. When fbmScale is zero (the default), there is no distortion. The remaining params are the same as for the fbm function.

ヒント

Voronoi types 1 through 5:

image0 image1 image2 image3 image4

注釈

cvoronoi returns a random color for each cell and pvoronoi returns the point location of the center of the cell.

選択関数

float choose ( float index, float choice1, float choice2, [...] )

Chooses one of the supplied choices based on the index (assumed to be in the range [0, 1]).

int cycle ( int index, int loRange, int hiRange )

Cycles through values between loRange and hiRange based on supplied index. This is an offset mod function. The result is computed as loRange + value % (hiRange-loRange+1).

int pick ( float index, int loRange, int hiRange, [ float weights, ... ] )

Picks values randomly between loRange and hiRange based on supplied index (which is automatically hashed). The values will be distributed according to the supplied weights. Any weights not supplied are assumed to be 1.0.

float wchoose ( float index, float choice1, float weight1, float choice2, float weight2, [...] )

Chooses one of the supplied choices based on the index (assumed to be in range [0, 1]). The values will be distributed according to the supplied weights.

ヒント

この例では1から10の整数値を返します:

pick(value, 1, 10)

この例では他の値(3-10)に比べ1と2をそれぞれ2倍と2.5倍返します:

pick(value, 1, 10, 2, 2.5)

この例では 10，11，13 から 20 を返します (12 は重み 0 のため除外されます):

pick(value, 10, 20, 1, 1, 0)

一般的な数学定数と関数

float PI
float PI = 3.14159...
float E
float E = 2.71828...
float abs ( float x)

x の絶対値。

float cbrt ( float x )

立方根。

float ceil ( float x )

次に大きな整数。

float exp ( float x )

E の x 乗。

float floor ( float x )

次に小さい整数。

float fmod ( float x, float y )

x / y の余り。

注釈

また % 演算子でも利用可能。

float log ( float x )

自然対数。

float log10 ( float x )

10を底とする対数。

float max ( float a, float b )

a と b の大きい方。

float min ( float a, float b )

a と b の小さい方。

float pow ( float x, float y )

x の y 乗。

注釈

また ^ 演算子でも利用可能。

float round ( float x )

最も近い整数。

float sqrt ( float x )

平方根。

float trunc ( float x )

0に近い方の整数。

三角関数

float acos ( float x )

逆余弦。

float acosd ( float x )

度数法での逆余弦。

float acosh ( float x )

双曲線逆余弦。

float asin ( float x )

逆正弦。

float asind ( float x )

度数法での逆正弦。

float asinh ( float x )

双曲線逆正弦。

float atan ( float x )

逆正接。

float atand ( float x )

度数法での逆正接。

float atan2 ( float y, float x)

-PI から PI の間での y/x の逆正接。

float atan2d ( float y, float x )

度数法での -180º から 180º の間での y/x の逆正接。

float atanh ( float x )

双曲線逆正接。

float cos ( float x )

余弦。

float cosd ( float x )

度数法での余弦。

float cosh ( float x )

双曲線余弦。

float deg ( float x )

ラジアンから度数法に。

float hypot ( float x, float y )

2Dベクトル [x, y] の長さ

float rad ( float x )

度数法からラジアンに。

float sin ( float x )

正弦。

float sind ( float x )

度数法での正弦。

float sinh ( float x )

双曲線正弦。

float tan ( float x )

正接。

float tand ( float x )

度数法での正接。

float tanh ( float x )

双曲線正接。

ベクトル関数

float angle ( vector a, vector b )

2つのベクトル間の角度 (ラジアン)。

vector cross ( vector a, vector b )

Vector cross product.

float dist ( vector a, vector b )

2点間の距離。

float dot ( vector a, vector b)

Vector dot product.

float length ( vector v )

ベクトルの長さ。

vector norm ( vector v )

Vector scaled to unit length.

vector ortho ( vector a, vector b )

Vector orthographic to two vectors.

vector rotate ( vector v, vector axis, float angle )

Rotates v around axis by the given angle (in radians).

vector up ( vector v, vector up )

Rotates v such that the Y axis points in the given up direction.

Vector Support

Vectors (points, colors, or 3D vectors) may be intermixed with scalars (simple floating point values). If a scalar is used in a vector context, it is replicated into the three components, e.g. 0.5 becomes [0.5, 0.5, 0.5].

If a vector is used in a scalar context, only the first component is used. One of the benefits of this is that all the functions that are defined to work with scalars automatically extend to vectors. For instance, pick, choose, cycle, spline, etc., will work just fine with vectors.

Arithmetic operators such as +, *, etc., and scalar functions are applied component-wise to vectors. For example, applying the gamma function to a map adjusts the gamma of all three color channels.

Curve Functions

Interpolation of parameter values to a set of control points is governed by the following functions.

color ccurve ( float param, float pos0, color val0, int interp0, float pos1, color val1, int interp1, [...] )

Interpolates color ramp given by control points at param. Control points are specified by triples of parameters pos_i, val_i, and interp_i.

ヒント

Interpolation codes are:

  • 0 - none

  • 1 - linear

  • 2 - smooth

  • 3 - spline

  • 4 - monotone (non-oscillating) spline

float curve ( float param, float pos0, float val0, int interp0, float pos1, float val1, int interp1, [...] )

Interpolates a 1D ramp defined by control points at param. Control points are specified by triples of parameters pos_i, val_i, and interp_i.

ヒント

Interpolation codes are:

  • 0 - none

  • 1 - linear

  • 2 - smooth

  • 3 - spline

  • 4 - monotone (non-oscillating) spline

float spline ( float param, float y1, float y2, float y3, float y4, [...] )

Interpolates a set of values to the parameter specified where y1, ..., yn are distributed evenly from [0, 1].

Custom Plugins

Custom functions may be written in C++ and loaded as one or more dynamic plugins. See Writing Custom Expression Plugins for more details.

警告

This functionality is not supported in Krita.