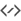取模运算

取模运算是一类特殊的混合模式。如果混合图层的某通道颜色数值小于基底图层，混合后得到的颜色数值会呈现出周期性变化。每一种取模运算混合模式都会在余数大于最大值或者小于最小值时保留余数的绝对值。对于连续性的取模运算模式，如果在取模运算之前算出的数值在奇数和偶数之间，则把结果数值进行反相，使得数值呈现出波状循环。

由于取模运算类混合模式的上述特征，它们在营造抽象效果和演绎特殊渐变方面有独特的应用价值。

取余运算

提示

此混合模式的英文名为“Divisive Modulo”。

首先把基底图层数值除以混合图层数值与大于零的最小可能数值的和。然后把该结果与混合图层数值与大于零的最小可能数值的和进行取模运算。

左图：基底图层，中图：混合图层，右图：取余运算混合结果。

取余运算 - 连续

提示

此混合模式的英文名为“Divisive Modulo - Continuous”。

首先把基底图层数值除以混合图层数值与大于零的最小可能数值的和。然后把该结果与混合图层数值与大于零的最小可能数值的和进行取模运算。最后把任何在奇数和偶数之间的结果进行反相处理，产生连续循环。

左图：基底图层，中图：混合图层，右图：取余连续混合结果。

取模运算

提示

此混合模式的英文名为“Modulo”。

用混合图层数值与大于零的最小可能数值的和进行取模运算。

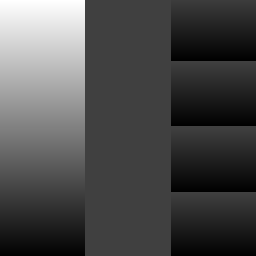
左图：基底图层，中图：混合图层，右图：取模运算混合结果。

取模运算 - 连续

提示

此混合模式的英文名为“Modulo - Continuous”。

用混合图层数值与大于零的最小可能数值的和进行取模运算。然后把任何在奇数和偶数之间的结果进行反相处理，产生连续循环。

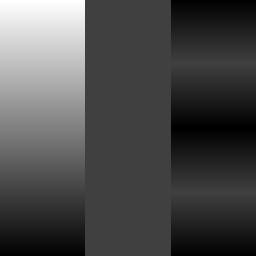
左图：基底图层，中图：混合图层，右图：取模连续混合结果。

取模运算偏移

提示

此混合模式的英文名为“Modulo Shift”。

用基底图层数值与混合图层数值的和乘以混合图层数值与大于零的最小可能数值的和的结果进行取模运算。

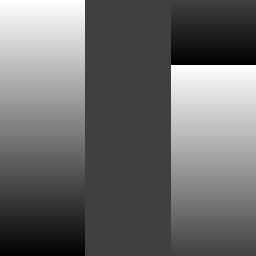
左图：基底图层，中图：混合图层，右图：取模偏移混合结果。

取模运算偏移 - 连续

提示

此混合模式的英文名为“Modulo Shift - Continuous”。

用基底图层数值与混合图层数值的和乘以混合图层数值与大于零的最小可能数值的和的结果进行取模运算。然后把任何在奇数和偶数之间的结果进行反相处理，产生连续循环。

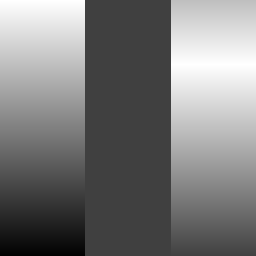
左图：基底图层，中图：混合图层，右图：取模偏移连续混合结果。