Bu, eksen ölçümsel öğreticisinin bir süreğidir, kafanız karışırsa bakmayı unutmayın!

Perspektif Projeksiyonu

Yani şimdiye kadar sadece paralel projeksiyon yaptık. Çizdiğimiz tüm projeksiyon çizgileri paralel olduğu için buna böyle denir.

Ancak gerçek hayatta paralel projeksiyon yoktur. Bunun nedeni gözümüzdeki mercektir.

Vikipedi’deki bu güzel görselin bize gösterdiği üzere, dışbükey mercekler paralel ışınları yakınsayan ışınlara dönüştürebilir.

Tüm ışınların birleştiği noktaya odak noktası denir ve 2 boyutlu bir çizimdeki ufuk noktası, iki paralel çizginin odak noktasına doğru eğildiğinde verilebilecek en çok bozulmanın ifadesi olduğu için bununla ilişkilidir.

Görselden de görebileceğiniz gibi odak noktası ışınların bitiş noktası değildir. Daha ziyade ışınların yeniden ayrılmadan önce kesiştiği yerdir… Tek fark ortaya çıkan görüntünün ters olmasıdır. Bu ters çevirme bizim gözlerimizde bile olur; ancak beynimiz çocukluğumuzdan beri bu tuhaflığa alışmıştır ve kendiliğinden çevirir.

Şimdi kutumuzu perspektif olarak yansıtabilir miyiz görelim.

Bu oldukça iyi gitti. Gördüğünüz gibi, iki kenarı bir şekilde birleştirdik (sonuçta mor yan kare elde ettik), böylece projeksiyonu daha kolay yaptık. Projeksiyon bir veya iki kaçış noktası türü projeksiyonla sınırlıdır, bu nedenle yalnızca yatay çizgiler bozulur. Üç noktalı bir projeksiyon elde etmek için…

… dikey çizgileri biraz daha bozabiliriz; ancak bu çok olurdu. (Orada bir yanlış yaptığımdan da eminim…)

Perspektif projeksiyonumuzu yeniden ayarlayalım…

Odak noktamız için tek bir ufuk noktası kullanacağız. Projeksiyon düzlemi için orada bir kılavuz çizgi olacak ve düz çizgileri görüş düzleminden kesiştikleri yere kolayca çizmek için yatay ve dikey paralel kurallar belirleriz.

GIF biçimindeki çalışma akışı için… (tuvali 4 ve 6 düğmeleriyle döndürebileceğinizi aklınızdan çıkarmayın)

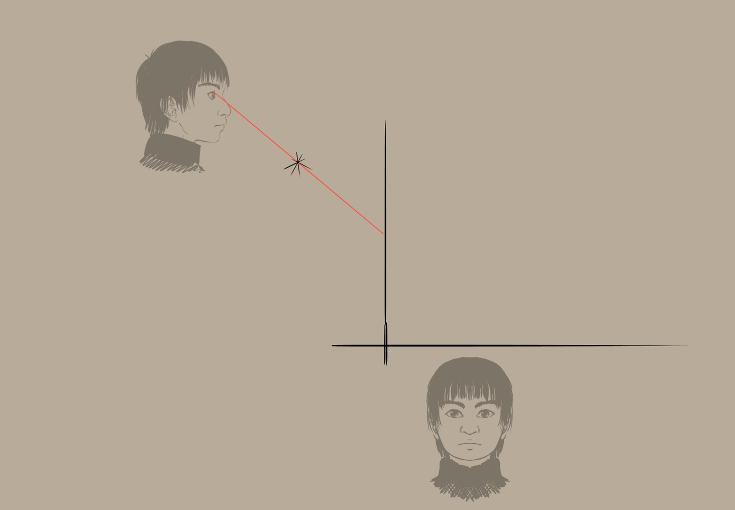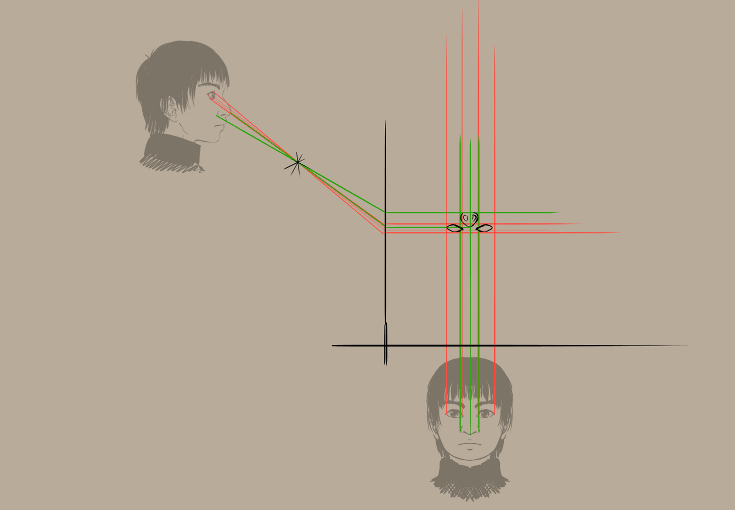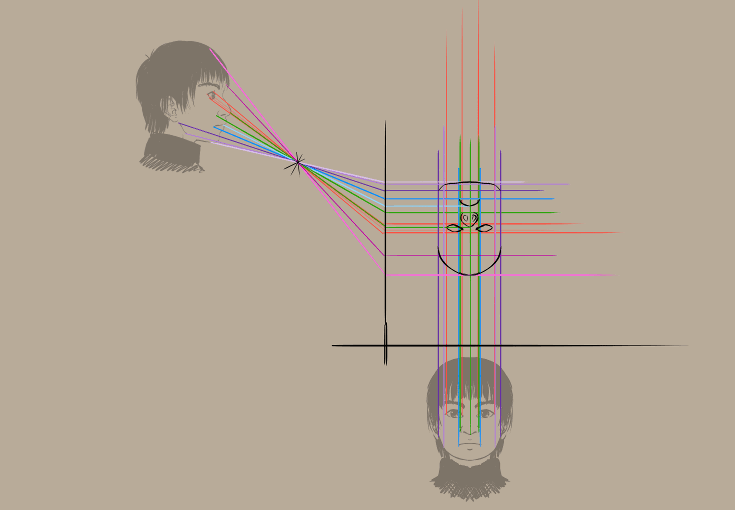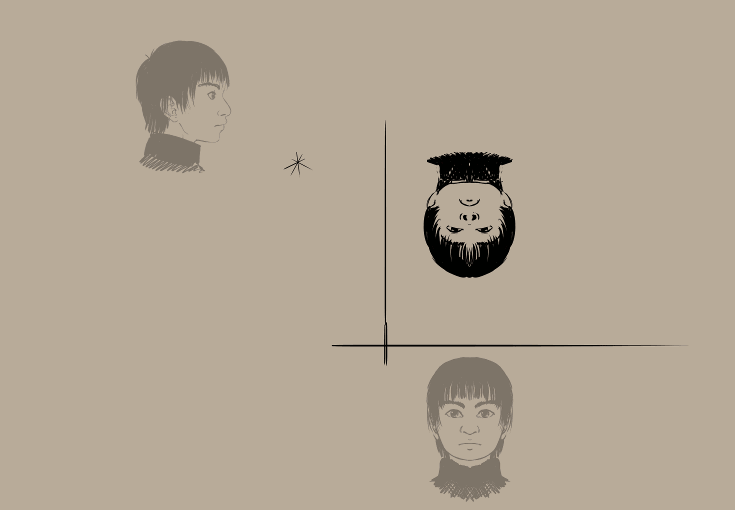
Sonuç:

Oldukça kibirli görünüyor, değil mi?

Ve yine, burada teknik olarak daha basit bir kurulum var…

3 boyutlu olarak döndürmek için Krita’yı kullanabileceğinizi biliyor muydunuz? Hayır?

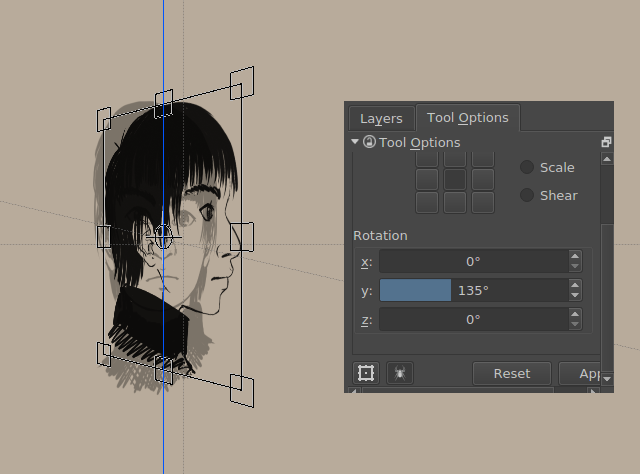
Artık şimdi biliyorsunuz.

Ortografik grafikler sırasıyla 45 ve 135 derecelik açılara ayarlanır.

Ufuk noktası cetvellerini onlara hizalayabilmemiz için özgünlerin üzerine yatay çizgiler çiziyoruz.

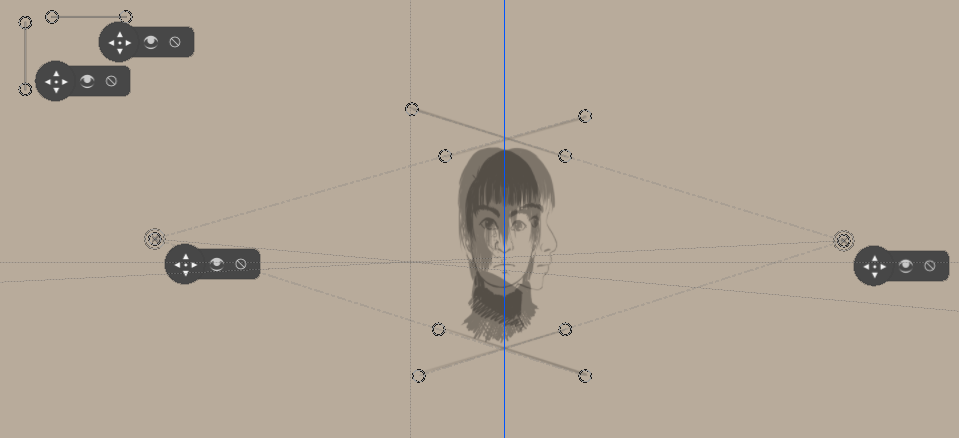
Ve bundan, kırkma yönteminde olduğu gibi, çizmeye başlıyoruz. (Üstten görünüşleri unutma!)

Bu, şöyle bir şey ortaya çıkarır:

Normal yöntem tabii biraz daha kolay…

Belki şöyle düşünüyor olabilirsiniz: Bu biraz çetrefilliymiş… Bilgisayarla bunu daha kolay yapamaz mıydık?

Evet, bu yüzden geliştiriciler 3B grafik teknolojisini geliştirmek için bu kadar uğraşıyorlar:

(Yukarıdaki görsel, ortografik başvurumuzu kullanarak Blender’da şekillendirilmiştir)

Bu tekniğin ne için kullanılabileceğine bir sonraki kısımda bakalım…