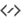Jest to część dalsza samouczka aksonometrii, upewnij się, że go przeczytałeś, gdy się zatniesz!

Rzutowanie perspektywy

Tak więc do tej pory rzutowaliśmy tylko równolegle. Nazywa się to tak dlatego, że wszystkie linie rzutowane, które rysowaliśmy były równoległe.

Jednakże, w rzeczywistym życiu nie mamy równoległych rzutowań. To ze względu na soczewkę w naszych oczach.

Wypukłe soczewki, jak ten uroczy obraz z wikipedi pokazują nam możliwość przekształcenia równoległych promieni światła na zbieżne.

Punkt, w którym wszystkie promienie zbiegają się w jeden jest nazywany ogniskową, a zanikający punkt na rysunku 2D jest z nim związany, jako iż jest to wyrażenie maksymalnego odkształcenia, które można nadać dwóm równoległym liniom, które są skrzywione względem ogniskowej.

Jak możesz zauważyć z obrazu, ogniskowa nie jest punktem końcowym promieni. Jest to raczej punkt przecięcia przed ich ponownym rozbiegnięciem… Jedyną różnicą jest to, że obraz wynikowy zostanie odwrócony. To odwrócenie dzieje się nawet w naszych oczach, lecz nasz mózg przyzwyczaił się do tej dziwności od małości, więc mimowolnie go obraca.

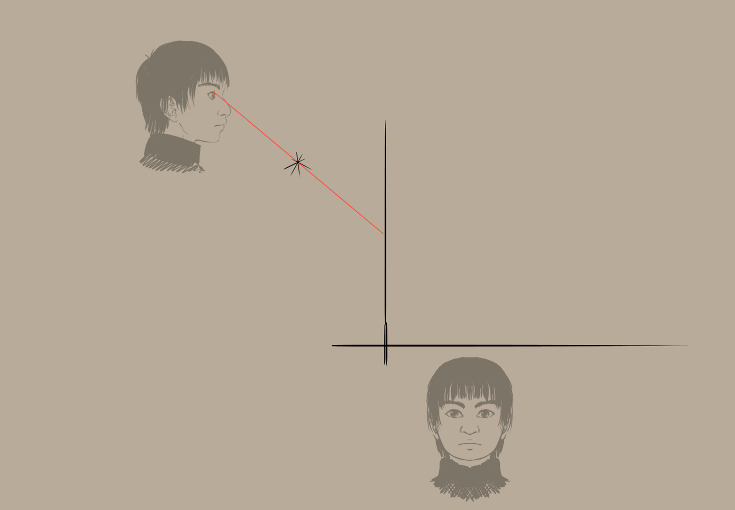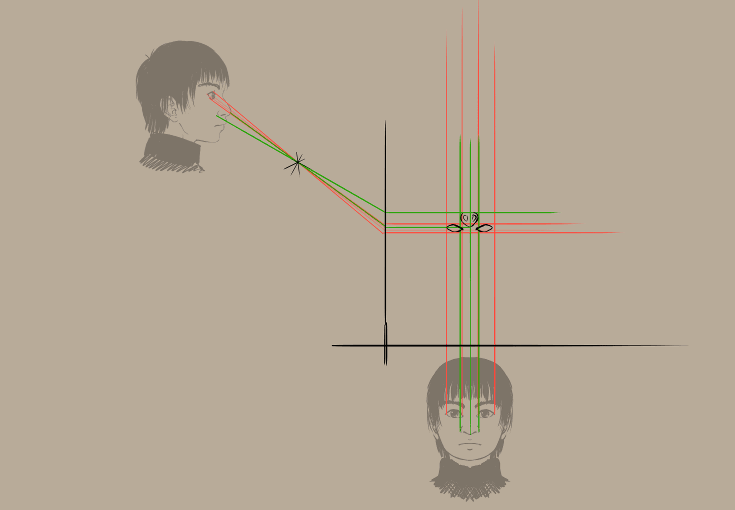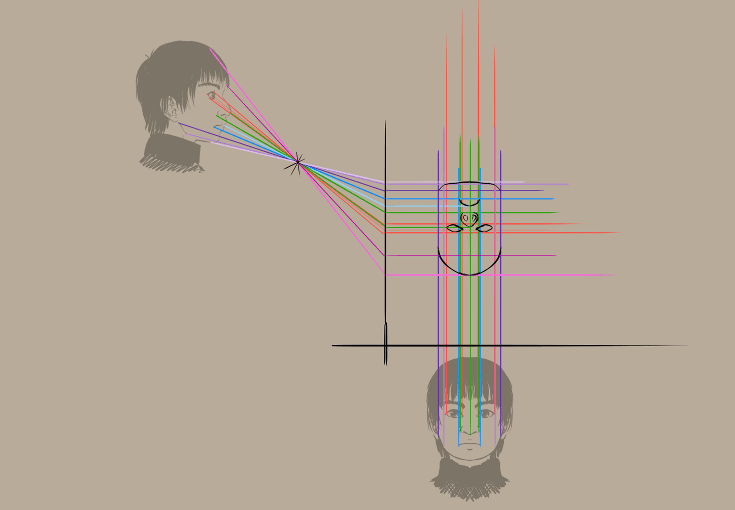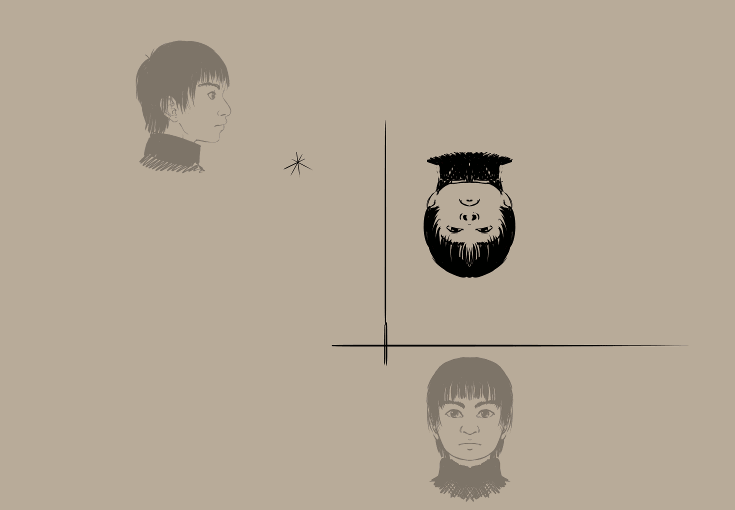
Zobaczmy, czy możemy teraz perspektywicznie rzutować nasze pudełko.

To poszło całkiem sprawnie. Jak widzisz, w pewnym sensie scaliliśmy dwa boki w jeden (co dało kwadrat o purpurowych bokach), tak aby łatwiej nam było go rzutować. Rzutowanie jest ograniczone do jednego lub dwóch rodzajów punktów zanikających, tak więc tylko linie w poziomie są zniekształcane. Możemy także zniekształcić linie w pionie

… aby uzyskać rzutowanie trzy-punktowe, lecz to jest trochę zbyt dużo. (Pomyliłem się też tutaj…)

Ustawmy na nowo narze rzutowanie perspektywiczne…

Będziemy używać pojedynczego punktu zanikającego dla naszej ogniskowej. Linia prowadząca będzie tutaj dla płaszczyzny rzutowania oraz nadamy zasady równoległości w poziomie i pionie, aby łatwo nam było narysować proste linie z płaszczyzny widoku do miejsca, w którym się przecinają.

A teraz przepływ pracy w formacie GIF… (nie zapominaj, że możesz obrócić płótno przy użyciu klawiszy 4 oraz 6)

Wynik:

Wygląda całkiem wyniośle, czyż nie?

I ponownie, technicznie jest tu prostsze ustawienie…

Czy wiedziałeś, że możesz użyć Krity do obrotu w 3D? Nie?

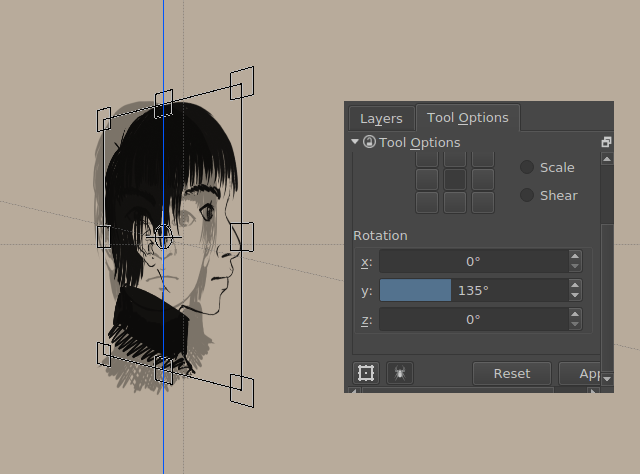
To teraz już wiesz.

Orto grafiki są ustawione odpowiednio na 45 i 135 stopi.

Rysujemy linie w poziomie jako pierwotne, tak że możemy wyrównać linijki zanikającego punktu z nimi.

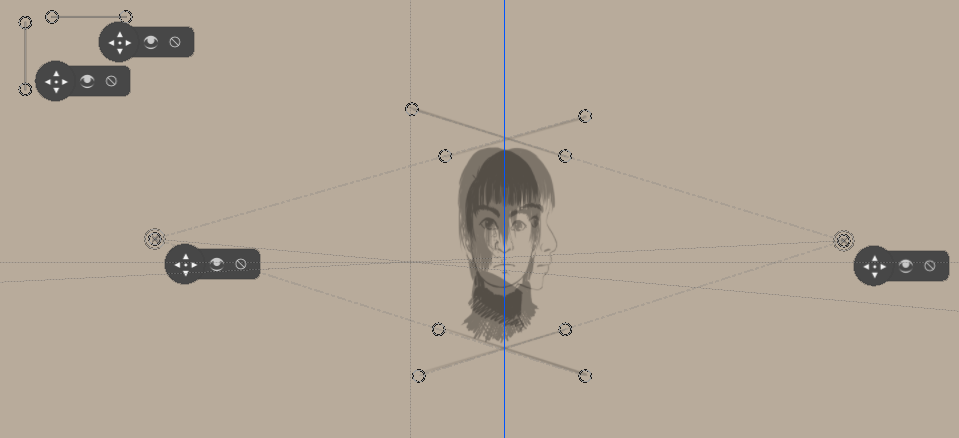
A z tego, tak jak w przypadku ścinania, rozpoczynamy rysowanie. (Nie zapominaj o widokach z góry!)

Co powinno ci dać coś na kształt:

Lecz znowu, zwykły sposób jest trochę prostszy…

Teraz jednak możesz zacząć myśleć: to jest jednak dużo pracy… Czy nie możemy tego jakoś uprościć na komputerze?

Właściwie, tak, jest to jeden z powodów, dla którego ludzie spędzali czas na rozwoju technologii grafiki 3D:

(Obraz powyżej został wyrzeźbiony w blenderze przy użyciu ortograficznych odniesień)

Tak więc przyjrzyjmy się do czego można praktycznie wykorzystać tę technikę w następnej części…