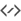In questa pagina continua l”esercitazione assonometrica, accertati di leggerla se hai dubbi!

Proiezione prospettica

Fino ad ora abbiamo lavorato con la proiezione parallela. È chiamata così perché tutte le linee di proiezione che abbiamo disegnato erano parallele.

Nella vita reale, tuttavia, non abbiamo proiezione parallela, a causa delle lenti presenti nei nostri occhi (cristallino).

Le lenti convesse, come ci mostra questa bella immagine presa da Wikipedia, hanno la capacità di trasformare i raggi di luce paralleli in convergenti.

Il punto in cui tutti i raggi convergono si chiama punto focale, e il punto di fuga in un disegno a due dimensioni è collegato ad esso, in quanto è l’espressione della massima distorsione che può essere data a due linee parallele quando vengono deviate verso il punto focale.

Come puoi notare nell’immagine, il punto focale non è il punto di arrivo dei raggi. È piuttosto il punto in cui i raggi si incontrano prima di divergere di nuovo… La sola differenza è che l’immagine risultante sarà invertita. L’inversione avviene anche nei nostri occhi, ma il nostro cervello è abituato a questa stranezza fin dalla nascita e gira (interpreta) l’immagine in modo automatico.

Ora vediamo se siamo in grado di progettare prospetticamente la nostra scatola.

È andata piuttosto bene. Come puoi notare abbiamo in un certo senso unito i due lati in uno (il risultato è il rettangolo viola), e questo ci ha semplificato il lavoro nella proiezione. Questa è limitata a una o due proiezioni di tipo punto di fuga, dunque vengono distorte solo le linee orizzontali. Possiamo distorcere anche le linee verticali

… per ottenere una proiezione a tre punti, ma questo è un po” troppo (e qui ho pure sbagliato completamente…).

Impostiamo di nuovo la nostra proiezione prospettica…

Per il nostro punto focale useremo un solo punto di fuga. Sarà presente una linea guida per il piano di proiezione, e imposteremo righelli paralleli orizzontali e verticali in modo da disegnare facilmente le rette dal piano della vista al punto dove intersecano.

E ora il flusso di lavoro in formato GIF… (non dimenticare che puoi ruotare la tela con i tasti 4 e 6)

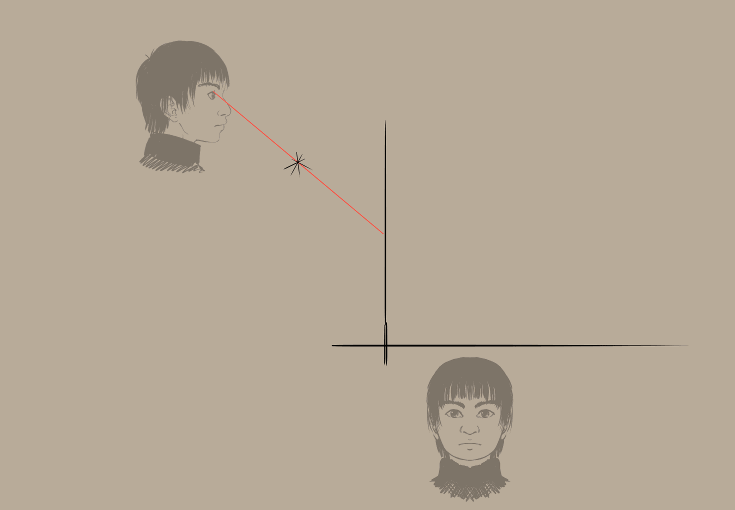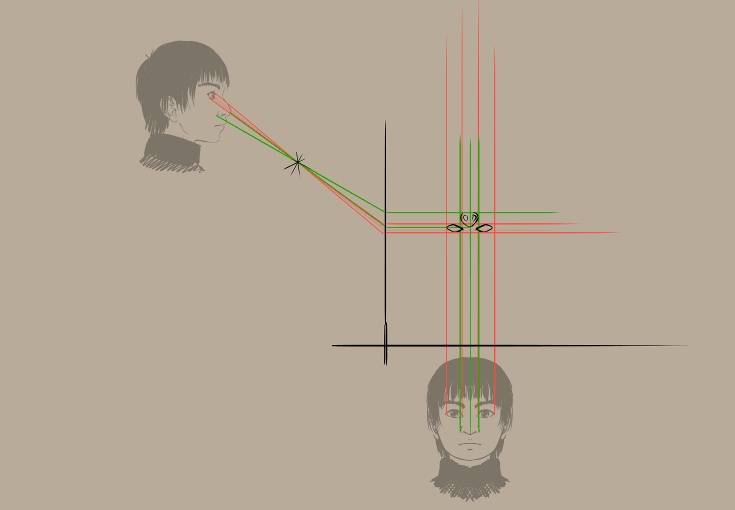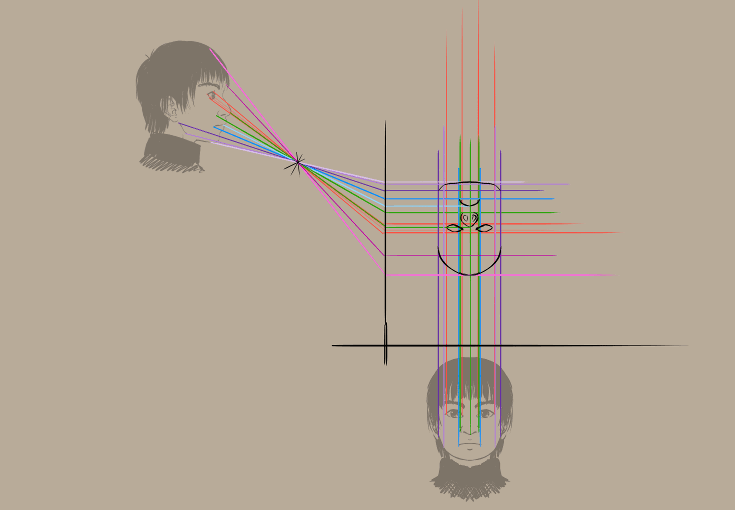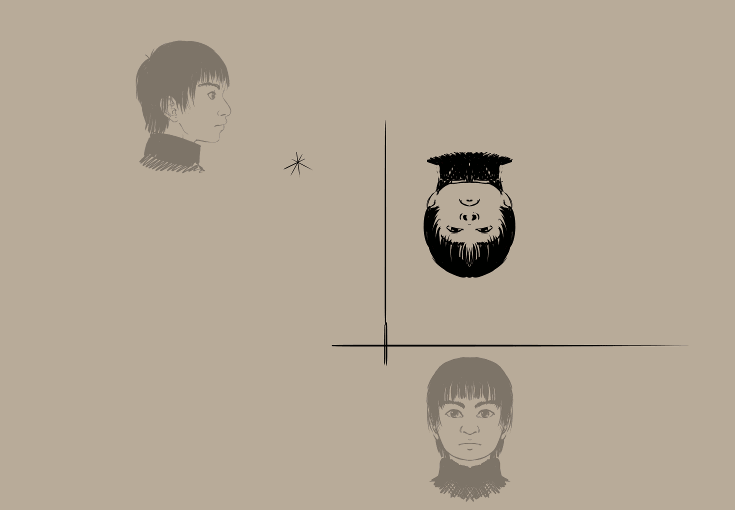
Risultato:

Sembra piuttosto altezzoso, vero?

Ripeto, esiste una configurazione tecnicamente più semplice qui…

Sai che puoi usare Krita per ruotare in 3D? No?

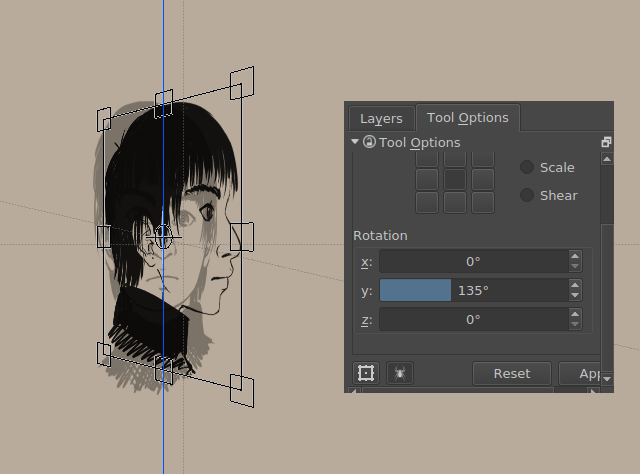
Bene, ora lo sai.

Le immagini delle direttrici sono impostate rispettivamente a 45° e 135°.

Disegniamo le righe orizzontali sugli originali, in modo da poter allineare a esse i righelli dei punti di fuga.

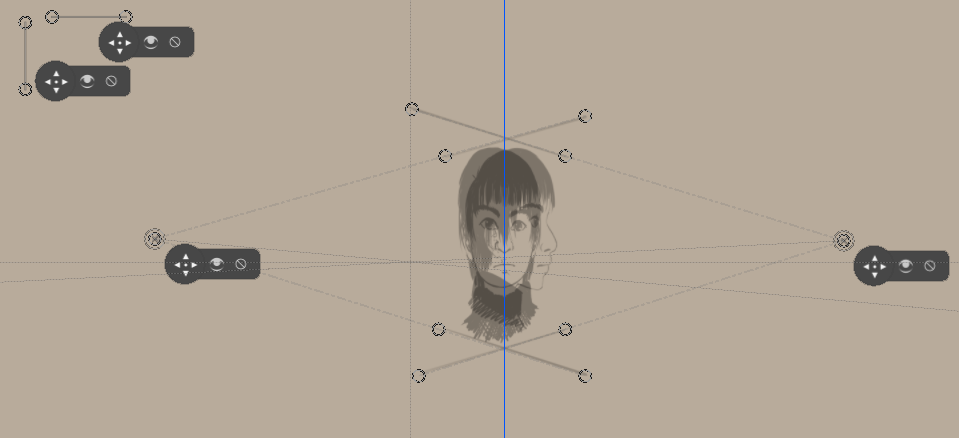
E da questo, come col metodo di deformazione, iniziamo a disegnare (non dimenticare le viste dall’alto!).

Dovresti ottenere qualcosa di simile a questo:

Di nuovo, il metodo normale è in realtà un po” più semplice…

Ora starai pensando: cavolo, ma è sacco di lavoro… Posso renderlo in qualche modo più semplice col computer?

Sì, ecco perché le persone si preoccupano di sviluppare la tecnologia grafica 3D:

(L’immagine riportata sopra è scolpita in Blender utilizzando i nostri riferimenti ortografici)

Nella prossima parte vedremo dunque come mettere in pratica questa tecnica…