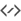Ceci est la poursuite du tutoriel axonométrique. Veuillez vous assurer de le lire si vous êtes un peu perdu !

Projection en perspective

Ainsi, jusqu'à présent, seule la projection parallèle a été réalisée. Elle est appelée comme cela car toutes les lignes de projection dessinées ont été des parallèles.

Toutefois, dans la vraie vie, il n'y a pas de projection parallèle. Ceci provient de l'effet de lentille dans les yeux.

Les lentilles convexes, comme cette magnifique image de « Wikipedia <https://fr.wikipedia.org/wiki/Lentille_optique> »_ le montre, ont la capacité de traiter les rayons lumineux parallèles pour les faire converger.

Le point vers lequel tous les rayons lumineux convergent est appelé le point focal. Le point de fuite dans un dessin en 2D lui est lié, puisqu'il est l'expression de la distorsion maximale appliquée à deux lignes parallèles pour être dirigées vers le point focal.

Comme indiqué sur l'image, le point focal n'est pas le point final des rayons lumineux. C'est plutôt l'endroit où les rayons se croisent avant de diverger à nouveau. La seule différence est que l'image résultante sera inversée. Même au niveau de vos yeux, cette inversion se fait mais votre cerveau est habitué à cet inconvénient depuis votre petite enfance et le corrige automatiquement.

Voyons si une projection en perspective de votre boîte est possible.

Cela s'est plutôt bien passé. Comme vous pouvez le voir, les deux côtés sont fusionnés en un (avec le résultat d'un carré avec des côtés violets). Ainsi, la projection sera faite avec moins de temps. La projection est limitée à une projection avec un ou deux types de points de fuite. En conséquence, les lignes horizontales seront déformées. Les lignes verticales peuvent elles aussi être déformées.

...pour obtenir une projection en trois points, mais ceci est un peu trop. (Et j'ai vraiment fait une erreur à l'intérieur...)

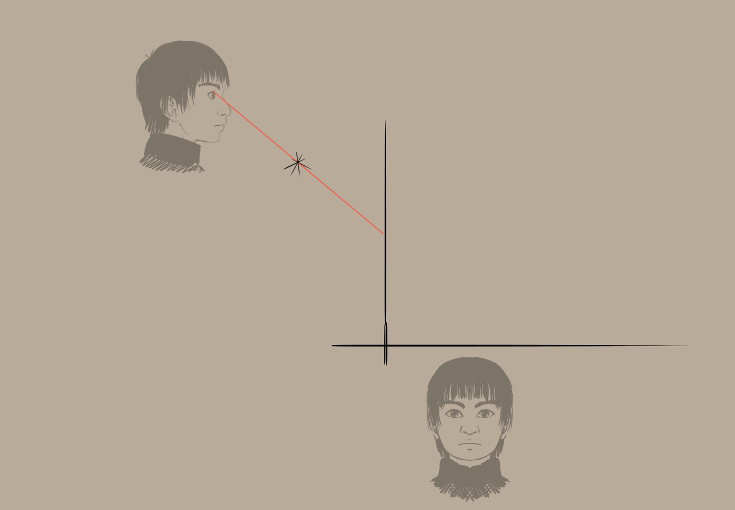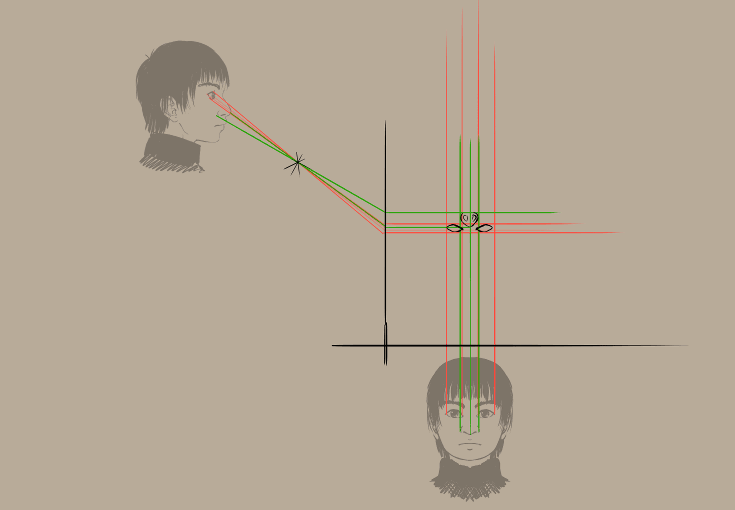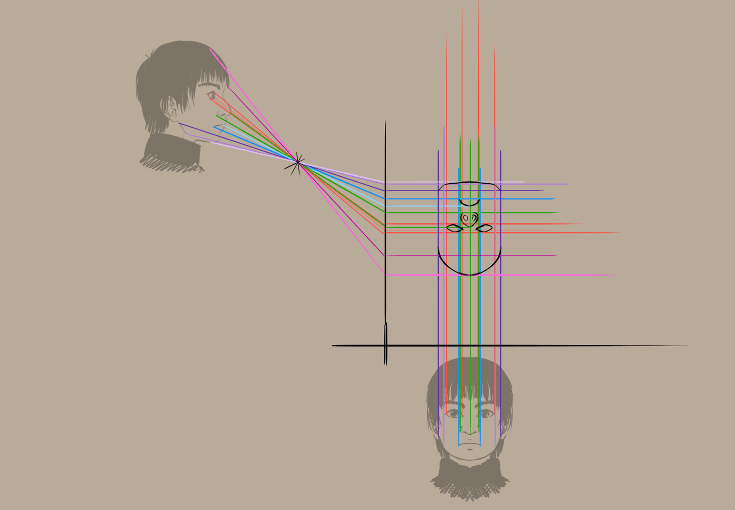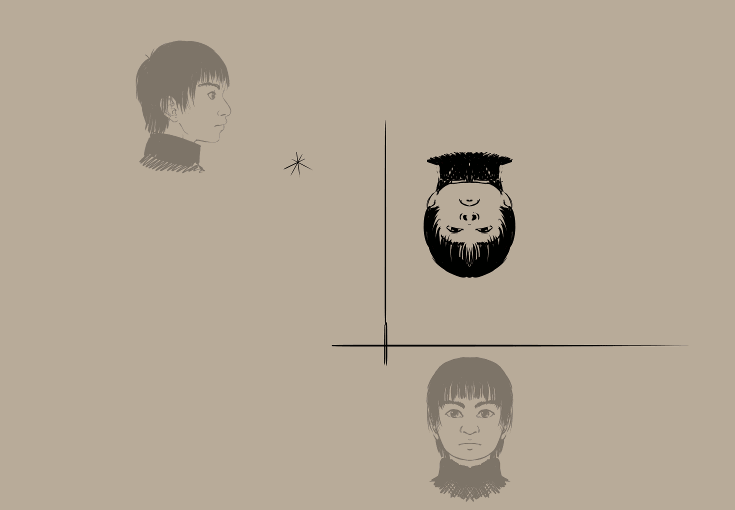
Re-définissez votre projection de perspective...

Un point unique de fuite sera utilisé comme point focal. Une ligne de guidage sera là pour le plan de projection. Des règles de parallèles verticales et horizontales sont définies pour facilement dessiner des lignes droites, partant du plan d'affichage vers l'endroit où elles se rejoignent.

Et maintenant, le flux de production en format « gif »... (Ne pas oublier que vous pouvez faire pivoter le tableau avec les touches 4 et 6).

Résultat :

Semble un peu prétentieux, n'est-ce pas ?

Et, de nouveau, il y a techniquement, un paramétrage plus simple ici...

Saviez vous que vous pouvez utiliser Krita pour des rotations en 3D ? Non ?

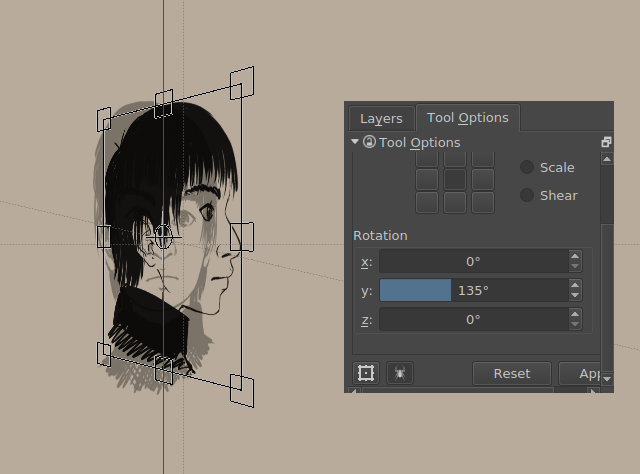
Eh bien, maintenant, vous le pouvez.

Les graphiques orthogonaux sont définis respectivement à 45 et 135 degrés.

Des lignes horizontales sont dessinées sur les originaux. Ainsi, les règles de points de fuite peuvent s'aligner dessus.

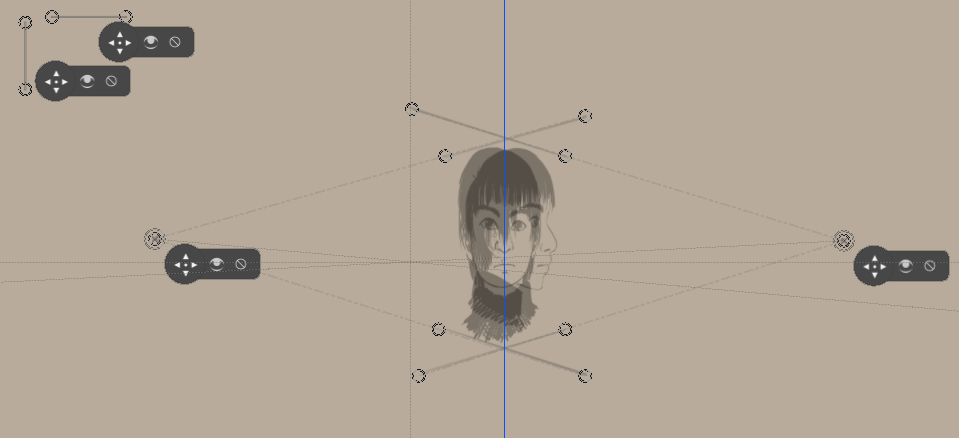
Et, à partir de ceci, comme avec la méthode de découpe, le dessin peut commencer (ne pas oublier les vues de dessus !)

Ce qui devrait vous donner quelque chose comme ceci :

Mais, de nouveau, la méthode classique est actuellement un peu plus facile...

Mais, maintenant, vous pourriez penser : zut, ceci fait beaucoup de travail... Est il possible, d'une certaine manière, de le rendre un peu plus facile avec l'ordinateur ?

Hum, oui, ceci est plus ou moins la raison pour laquelle les utilisateurs passent du temps pour le développement de technologies de graphisme 3D :

(L'image ci-dessus est façonnée dans Blender en utilisant la référence orthonormée)

Ainsi, regardons ce que cette technique peut apporter pratiquement pour la prochaine partie...