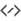Це продовження підручника щодо аксонометричної проєкції. Прочитайте його спершу, якщо щось у цьому розділі видасться вам незрозумілим!

Проєкція перспективи

Отже, досі ми мали справу із паралельними проєкціями. Назва цих проєкцій походить від того, що усі намальовані нами лінії проєкції були паралельними між собою.

Втім, у реальному світі проєкції не є паралельними. Причиною цього є лінзи наших очей.

Опуклі лінзи об’єктива, як показано на чудовому зображенні у Вікіпедії, мають властивість збирати паралельні промені світла у одній точці.

Точка, у якій сходяться промені називається фокальною точкою (фокусом), а нескінченно віддалену точку у плоских малюнках пов’язано із цією точкою, оскільки це зображення максимального викривлення, якого можна надати двом паралельним лініями при перекошуванні до фокальної точки.

Якщо можна бачити із рисунка, фокальна точка не є кінцевою точкою променів. Це лише точка, проходячи крізь яку промені знову розходяться… Відмінність полягає лише у тому, що зображення після цієї точки є перевернутим. Таке перевертання зображення відбувається і у наших очах, але мозок звик до нього з дитинства, отже виконує зворотне перевертання зображення автоматично.

Погляньмо, чи ми зможемо створити проєкцію перспективи з нашого паралелепіпеда.

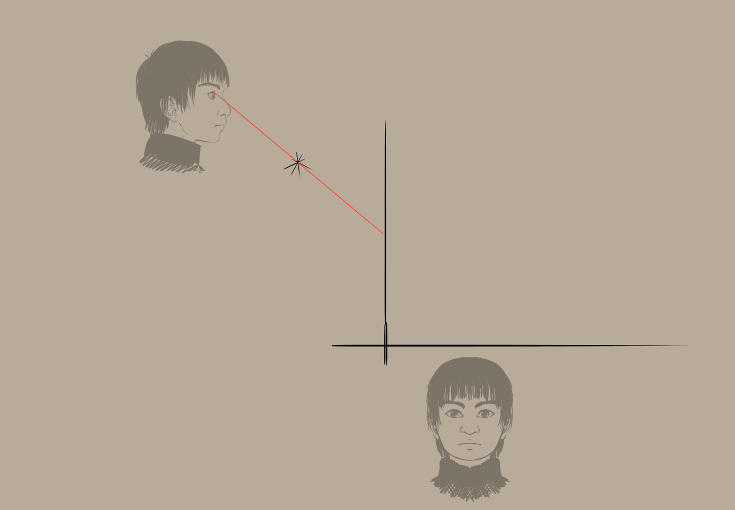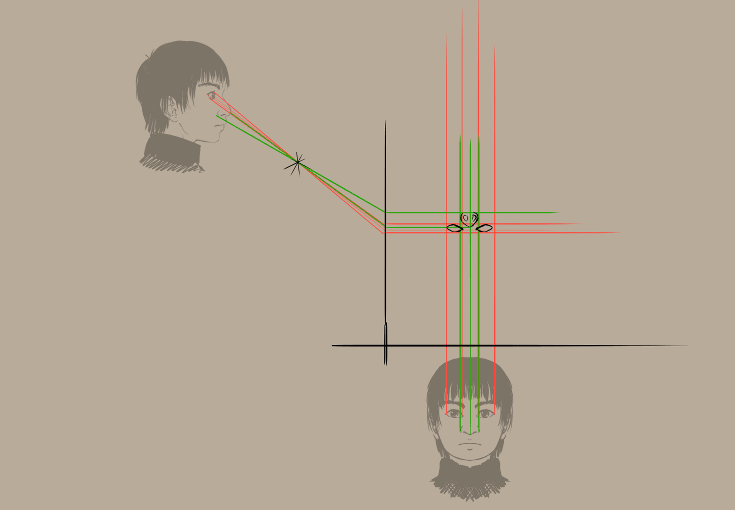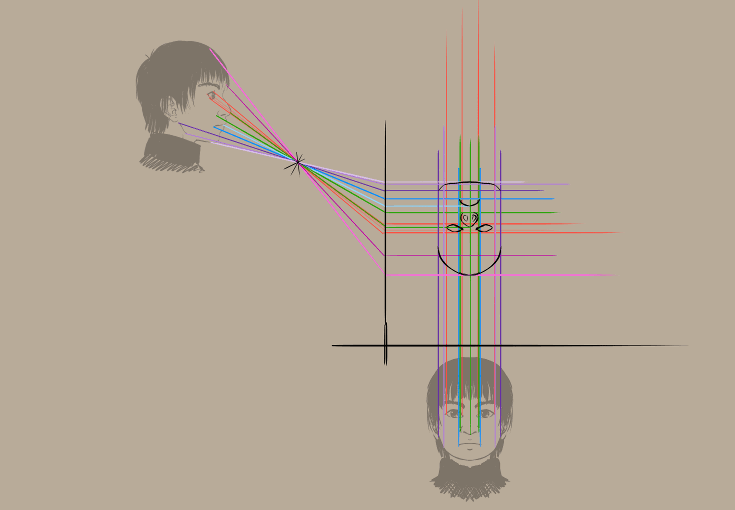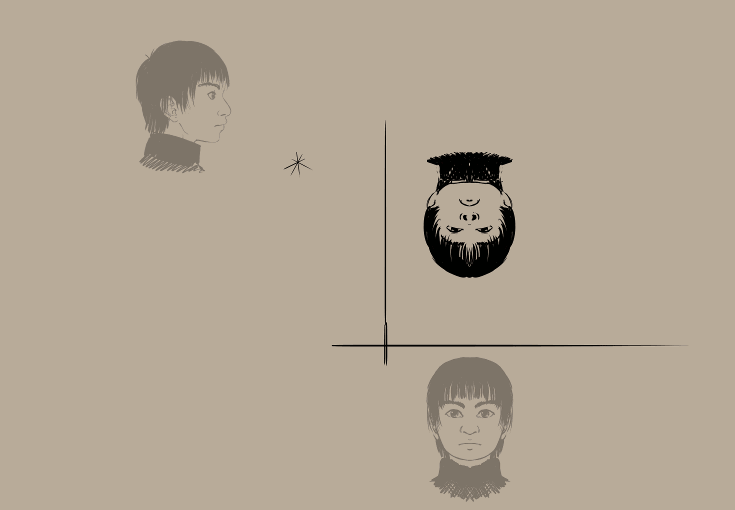
Вийшло доволі добре. Як можете бачити, ми певним чином «об’єднали» дві грані у одну (результат показано пурпуровим бічним прямокутником), щоб нам легше було проєктувати. Проєктування обмежено однією або двома проєкціями із нескінченно віддаленою точкою, отже викривляються лише горизонтальні лінії. Ми також можемо викривити і вертикальні лінії:

…щоб отримати триточкову проєкцію, але це занадто. (І загалом неправильно…)

Налаштуймо проєкцію перспективи ще раз…

Як фокальну точку, ми будемо використовувати одну нескінченно віддалену точку. Намалюємо напрямку для площини проєктування і налаштуємо горизонтальну і вертикальну паралельні лінійки для спрощення малювання прямих ліній з площини перегляду до точки перетину.

А тепер, робоча процедура у форматі GIF… (не забувайте, що полотно можна обертати за допомогою клавіш 4 та 6)

Результат:

Хлопець виглядає зарозумілим, чи не так?

І знову ж, технічно, можна зробити усе простіше…

Чи ви знали, що Krita можна скористатися для просторового обертання? Ні?

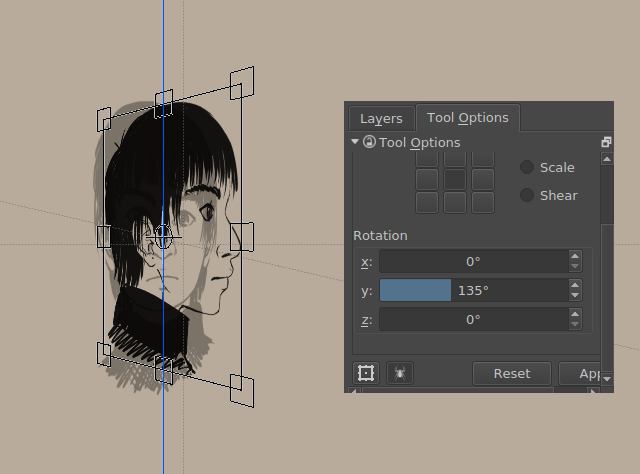
Гаразд, тепер ви знаєте, що це можна робити.

Значення для обертання встановлено на 45 і 135 градусів відповідно.

Ми намалювали горизонтальні лінії на оригіналах, щоб вирівняти за ними лінійки нескінченно віддаленої точки.

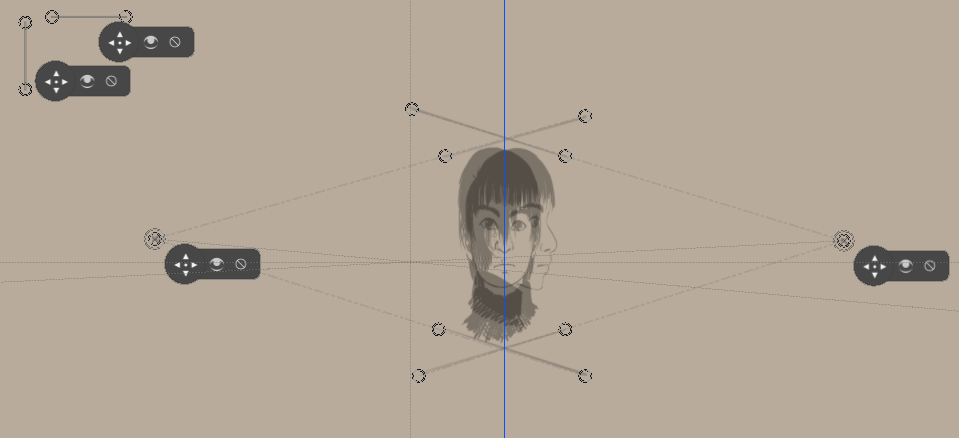
І, починаючи звідси, подібно до методу перекошування, розпочнімо малювати. (Не забудьте про вид згори!)

Що дасть вам щось таке:

Втім, знову ж таки, звичайний спосіб, насправді, трохи простіший…

Тепер, у вас може виникнути думка: «Оце тобі, доволі багато роботи… Чи не можна її якось полегшити за допомогою комп’ютера?»

Угу, звичайно ж, саме на це розробники витрачають час на розробку технологій тривимірної графіки:

Наведене вище зображення оброблено у Blender за допомогою нашого ортографічного еталона.

На практичне використання цієї методики ми поглянемо у наступному розділі підручника…