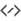Це продовження сторінки щодо ортографічної та похилої проєкцій. Щоб уникнути непорозумінь, спочатку ознайомтеся із попередніми сторінками!

Аксонометрична проєкція

Отже, логіка додавання виду згори є подібною до логіки додавання виду збоку.

Не дуже цікаво. Але усе стає набагато цікавішим, якщо ми скористаємося бічною проєкцією:

Оскільки наш паралелепіпед є червоним з обох передніх боків і синім з лівого і правого боків, ми можемо просто скористатися копіями. Це значно спрощує наш метод для паралелепіпедів. Ми називаємо цю форму аксонометричної проєкції «диметрією» оскільки вона деформує однаково дві паралельні лінії.

Ізометрія є подібною до диметрії, де ми маємо один кут між усіма основними лініями:

Істина ізометрія утворюється кутом 90-54.736=35.264° від площини основи:

(як можна бачити, вирівнювання не є ідеальним, оскільки в Inkscape, хоча ця програма і є придатнішою для створення такого типу діаграм, ніж Krita, немає інструментів для визначення кута відхилення ліній у градусах)

Це дещо незручний кут і, окрім того, він не дуже добре вирівнюється за пікселями. Тому у відеоіграх використовують кут 30° від площини основи.

Гаразд, тепер створимо ізометрію з нашого зображення голови хлопчика.

Ми створимо документ і додамо векторний шар.

На векторному шарі ми виберемо інструмент малювання прямої, розпочнемо малювати пряму, а потім натиснемо клавішу Shift для прилипання лінії до кутів. Це надасть нам змогу створювати лінії під кутом 30°, як у прикладі вище:

Далі, імпортуємо деякі кадри з анімації за допомогою пункту меню Шари ‣ Імпортування/Експортування ‣ Імпортувати шар.

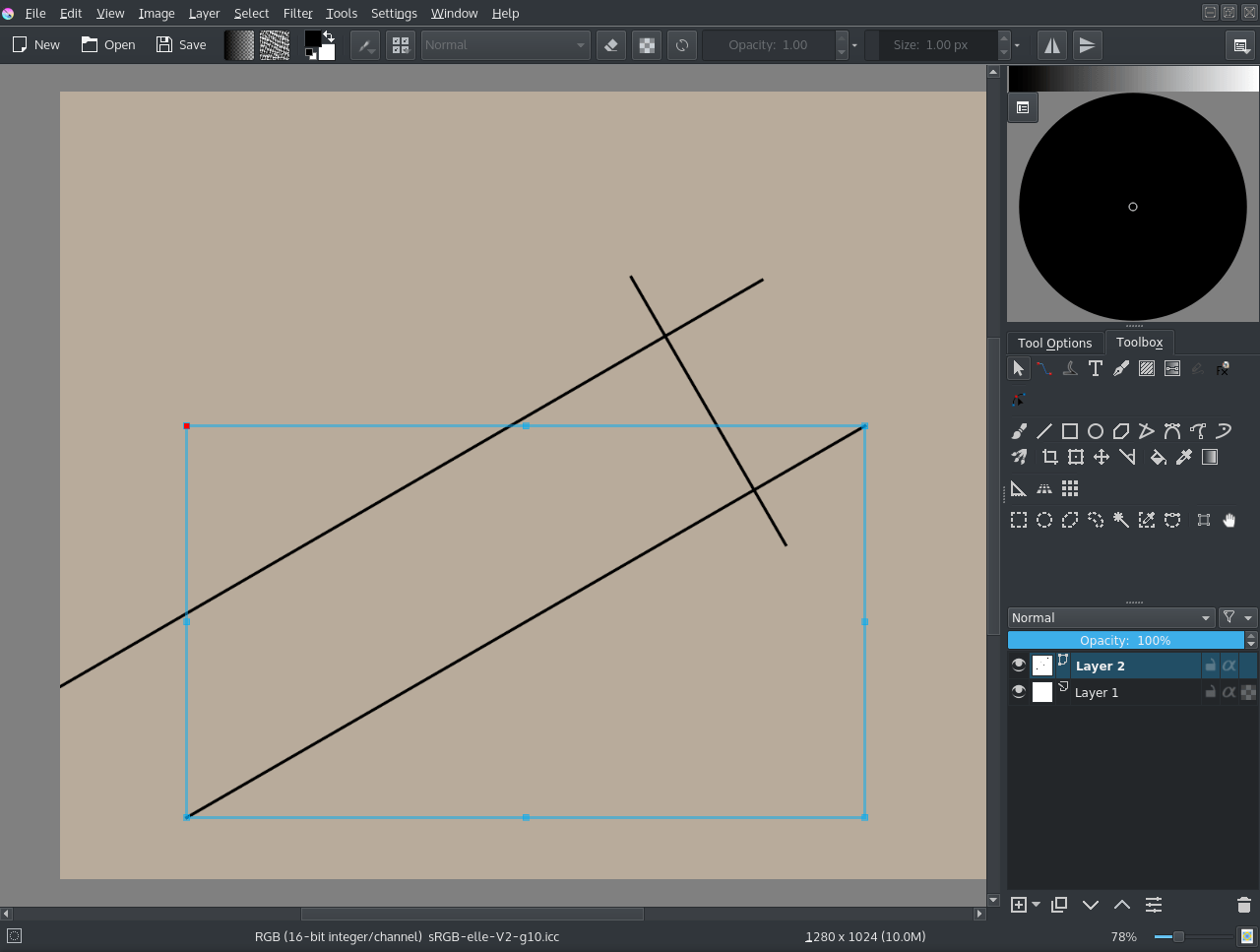
Потім обріжемо його встановленням для інструмента обрізання значення Шар і вибором пункту меню Фільтри ‣ Кольори ‣ Колір до альфи… для вилучення тла. Також автор встановив для шарів 50% непрозорості. Потім вирівняв вектори за головами:

Порада

Щоб змірити розміри вектора, але зберегти його напрямок, ви можете позначити його за допомогою вказівника інструмента роботи з формами (білої стрілочки), почати перетягувати один з кутів обмежувальної рамки вектора, а потім натиснути клавішу Shift, щоб зафіксувати співвідношення розмірів форми. Це надасть вам змогу не змінювати кут напрямку вектора.

На нижчому зображенні показано «вид на задню частину спереду». Ми скористаємося ним для визначення місця для вуха.

Далі, у нас, очевидно, замало місця. Тому виберемо інструмент обрізання, виберемо Зображення, позначимо пункт Збільшити і зробимо так:

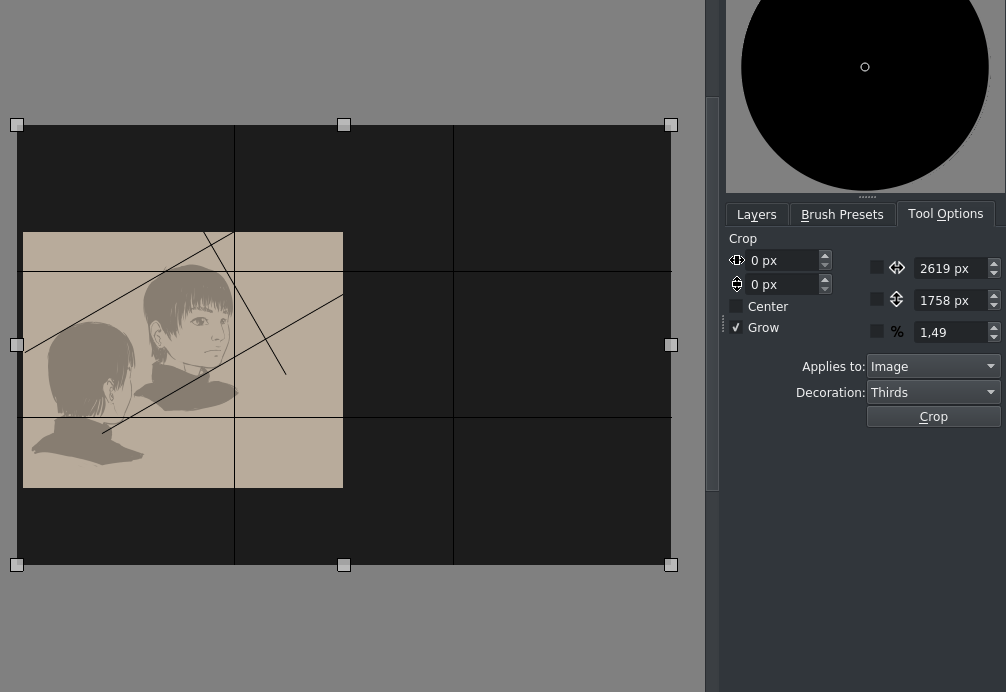
Збільшення є практичнішим способом негайної зміни розмірів полотна за шириною і висотою.

Далі, вирівняємо інші голови і перетворимо їх за допомогою параметрів інструмента перетворення:

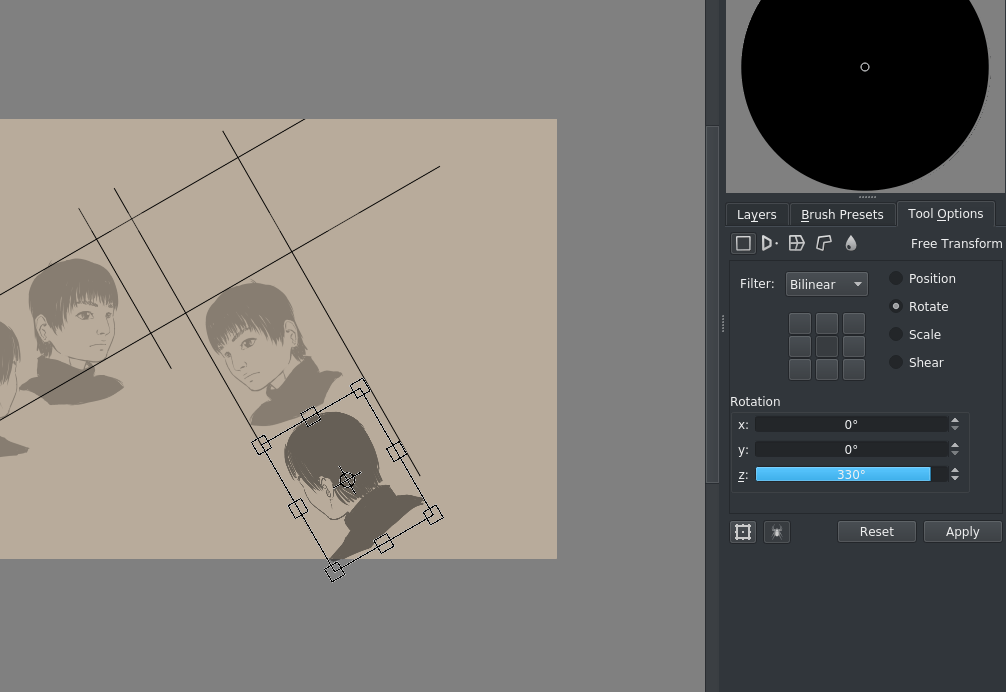
(330° тут це 360°-30°)

Наш прямокутник, над яким ми працюватимемо, повільно стає видимим. Оскільки його розташовано під незручним для роботи кутом, ми повернемо його за допомогою пункту меню Зображення ‣ Обернути ‣ Обернути зображення, вказавши обертання у 30° за годинниковою стрілкою:

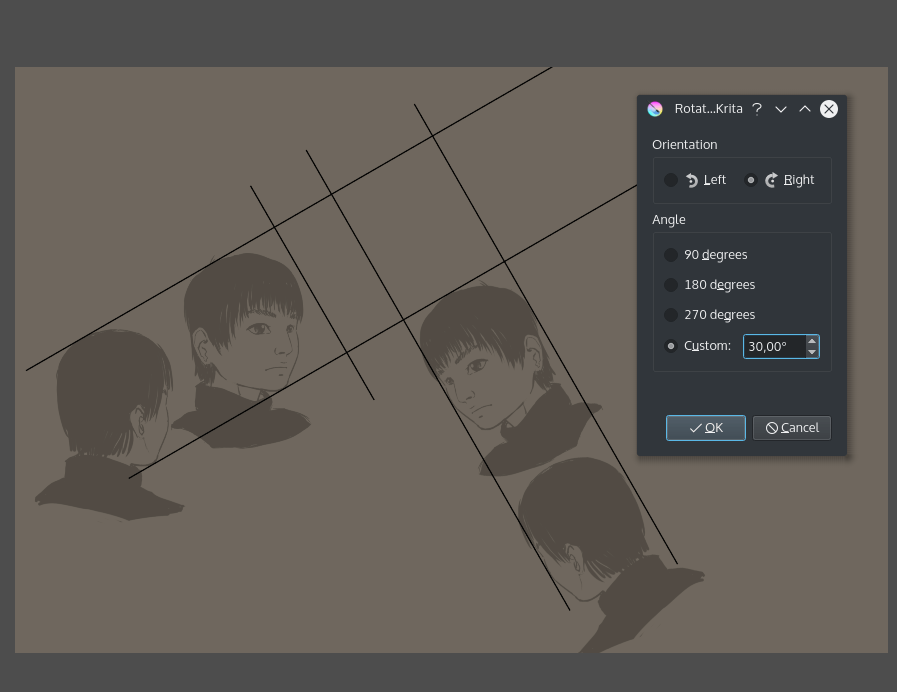
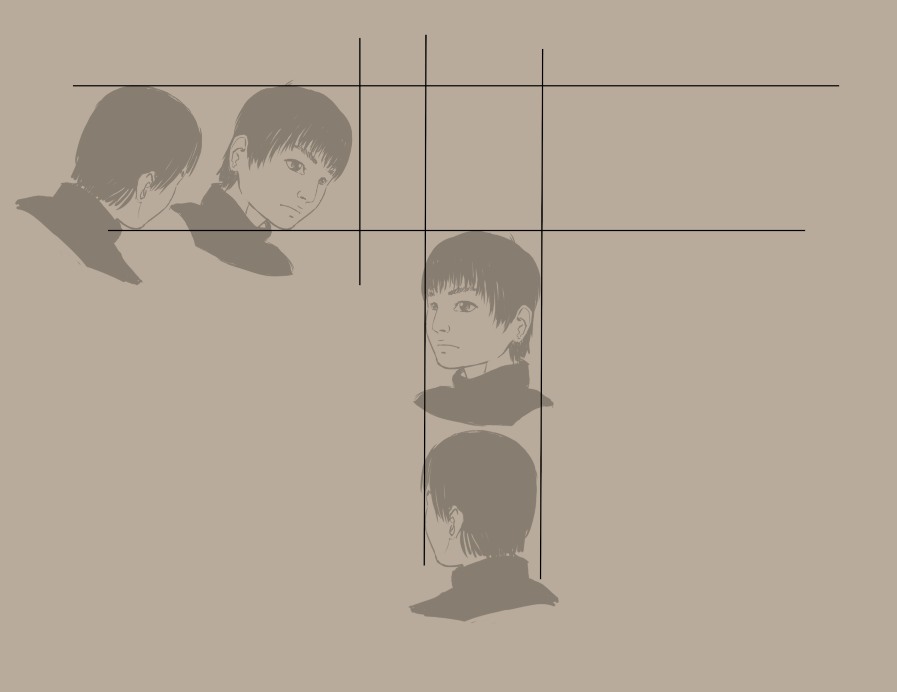
(звичайно ж, ми могли б просто повернути два зображення ліворуч на 30°, це, здебільшого, простіше за роботу з паралелепіпедом)

Отже, ми виконали певне обрізання, чищення і додали дві допоміжні паралельні лінії, як це було раніше зроблено для ортографічної проєкції:

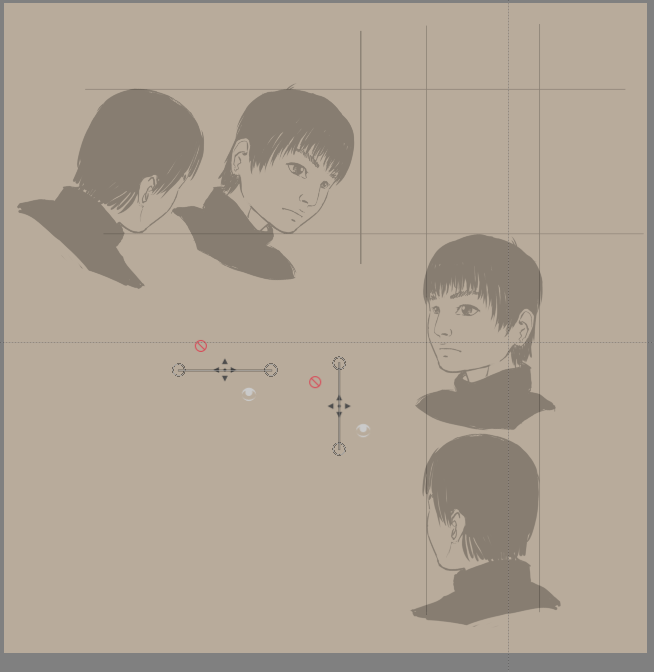
Отже, ідея полягає у малюванні паралельних ліній з обох боків для пошуку точок на ділянці малювання. Ви можете скористатися просто попередніми переглядами допоміжних ліній, щоб не захаращувати зображення зайвими лініями, але автор намалював ці лінії, щоб зручніше було зрозуміти принципи роботи.

Найкраще створити декілька точок-зразків, як ми це зробили у нашому прикладі для брів, а потім намалювати за ними брови.

Альтернативна аксонометрія із інструментом перетворення

Тепер скористаємося альтернативним способом отримання зображення, який не потребує багато місця.

Ми відкриємо наші ортографічні проєкції за допомогою пункту меню Відкрити наявний документ як документ без назви, щоб не зберігати зміни до початкового варіанта.

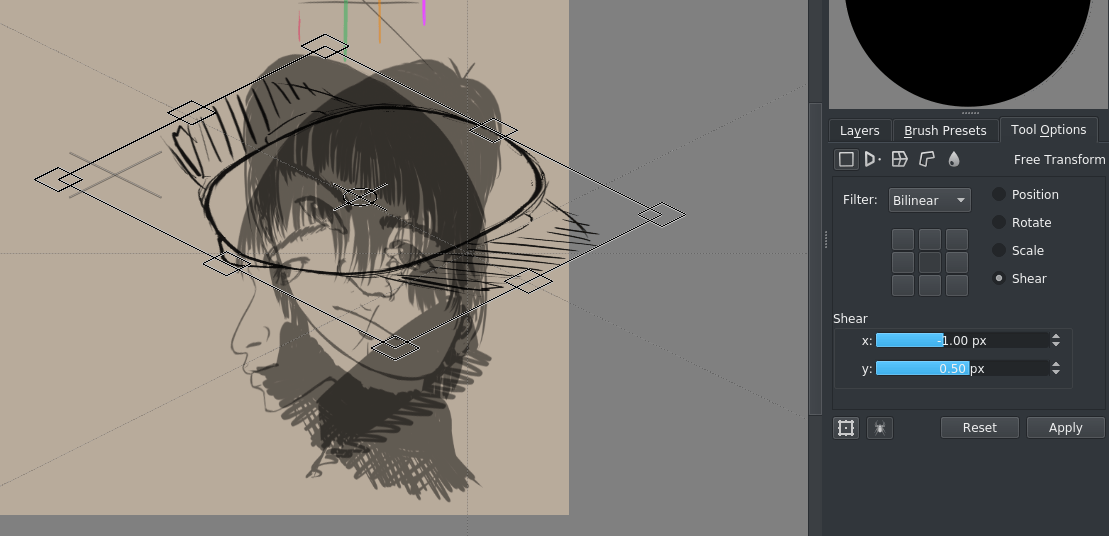
Наша призначена для відеоігор ізометрія має вісі, які розташовано так, що двом пікселям за горизонталлю відповідає один піксель за вертикаллю. Отже, ми перекосимо графіку за допомогою масок перетворення до -.5/+.5 пікселів (пропорційно).

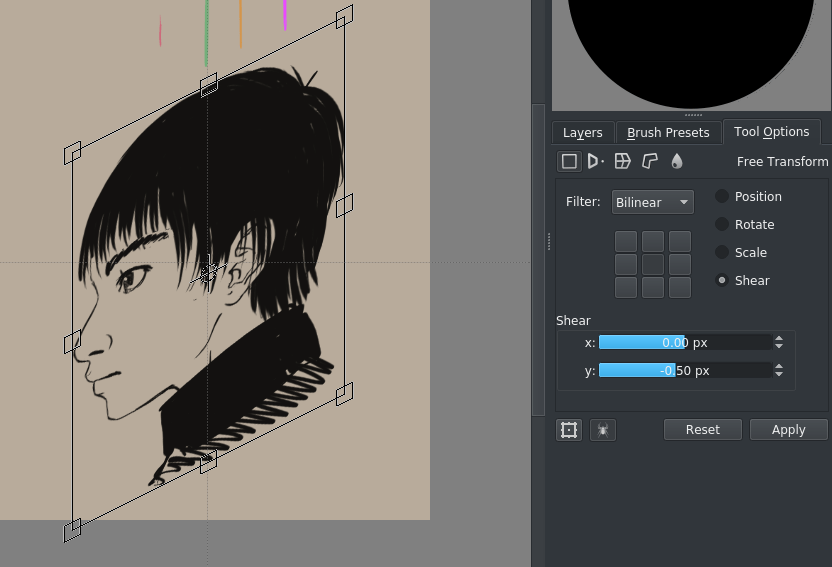
Скористаймося ґраткою для додавання двох паралельних лінійок, які відповідають обом діагоналями (ви можете увімкнути для них прилипання за допомогою комбінації клавіш Shift + S):

Додамо також вид згори:

якщо ви зробили це для усіх перерізів, у вас вийде щось таке:

Далі, за допомогою паралельних лінійок ви можете визначити розташування точки у просторі:

Як бачите, ця версія одночасно виглядає більш просторовою і страхітливою.

Причиною є те, що ми виконали менше кроків, порівняно із попередньою версією. Ми створили наше зображення безпосередньо на основі ортографічних проєкцій, отже зменшили похибку.

Певна страхітливість є наслідком того, що ми використали дещо стилізований вид збоку, тому очі вийшли ВЕЛИЧЕЗНИМИ. Це тому, що стилізуючи вид збоку ока ми намагалися намалювати його не зовсім збоку, а під певним кутом. Якщо ви поглянете уважніше на обертальний круг, ви зможете помітити там ту саму проблему.

Загалом кажучи, стилізація псує просторові форми. Ймовірно, вам доведеться робити певний вибір щодо її використання, щоб мати змогу користуватися проєкціями.

Наприклад, ми можемо просто виправити вид збоку (це просто, оскільки ми використовували маски перетворення).

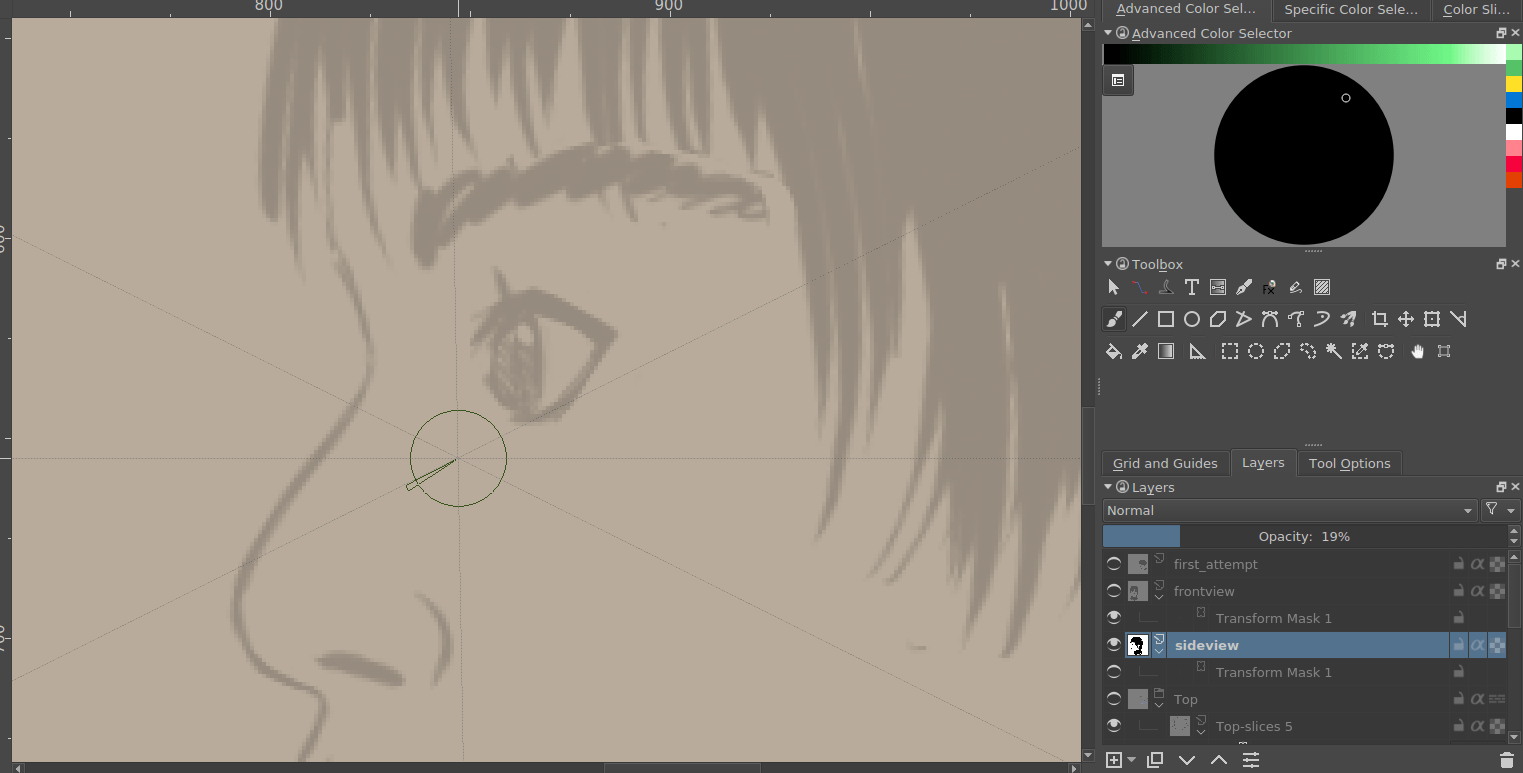
А потім створити з цього новий малюнок…

Порівнюючи попередній результат із цим, маємо зауважити, що очі у нового результату не такі страхітливі:

Результат виглядає дещо стиснутим, порівняно із результатом звичайної паралельної проєкції, наведеним вище. Тому варто не лише перекосити ортографічні проєкції, а і дещо розтягнути їх.

У наступному розділі ми продовжимо вправлятися зі проєкцією перспективи!