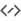Dit is een vervolg op de axonometrische inleiding, lees het als u het niet meer goed weet!

Perspectivische projectie

Tot nu toe hebben we alleen parallelle projectie bekeken. Dit wordt zo genoemd omdat alle projectielijnen die we tekenden parallel liepen.

In het echte leven hebben we geen parallelle projectie. Dit komt door de lenzen in onze ogen.

Convexe lenzen, zoals dit lieflijke plaatje uit wikipedia ons toont, heeft de mogelijkheid om parallelle lichtstralen om te buigen naar convergerende.

Het punt waar alle stralen samenkomen wordt het focus genoemd, en het verdwijnpunt in een 2d tekening heeft een relatie daarmee omdat het de maximale verbuiging weergeeft dat twee parallelle lijnen kunnen hebben als ze naar het focus afbuigen.

Zoals u in de afbeelding kunt zien, is de focus niet het eindpunt van de stralen. Maar, het is waar de stralen elkaar kruizen voordat ze weer uit elkaar gaan… Het enige verschil is dat de resulterende afbeelding geïnverteerd zal zijn. Zelfs in onze ogen vindt deze invertering plaats, maar onze hersenen zijn al sinds onze jeugd hieraan gewend en keren het automatisch om.

Laten we kijken of we nu onze doos in perspectief kunnen projecteren.

Dat ging vrij goed. Zoals u kunt zien, hebben we de twee zijden min of meer samengevoegd in een (in het paarse zijvlak resulterend) zodat we het makkelijker konden projecteren. De projectie is beperkt tot een soort projectie met een of twee verdwijnpunten, zodat alleen de horizontale lijnen vervormt worden. We kunnen ook de verticale lijnen vervormen

… om een driepunt-projectie te krijgen, maar dat is een beetje veel. (En ik maakte werkelijk een fout hier…)

Laten we onze perspectief-projectie nog een keer opzetten…

We willen voor onze focuspunt een enkele verdwijnpunt gebruiken. Voor ons projectievlak is er een hulplijn, en we maken horizontale en verticale hulplijnen zodat we makkelijker rechte lijnen kunnen trekken vanuit het projectievlak naar waar ze elkaar kruizen.

En dan nu de werkvolgorde in GIF formaat… (vergeet niet dat u het werkvlak kan roteren met de 4 en 6 toetsen)

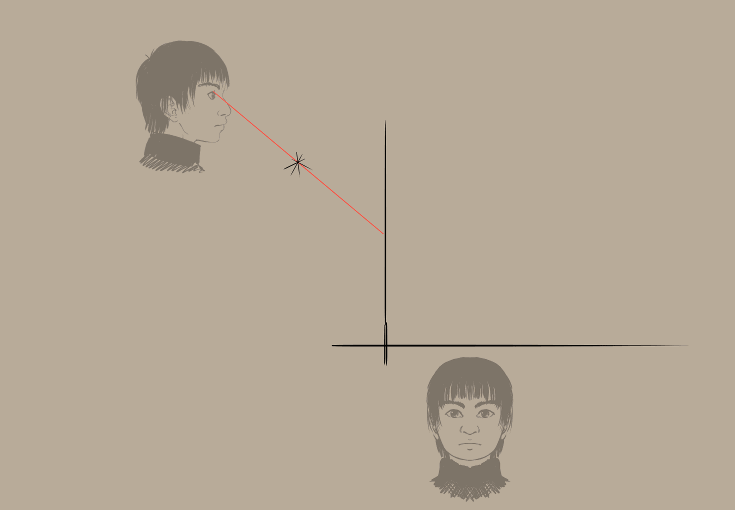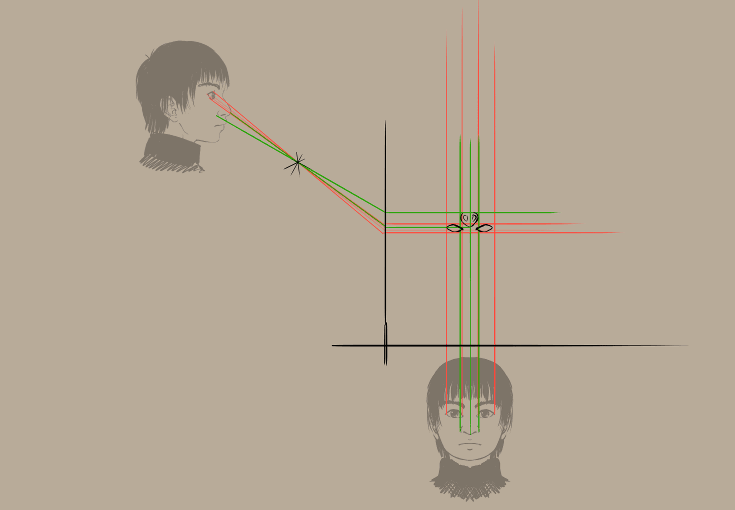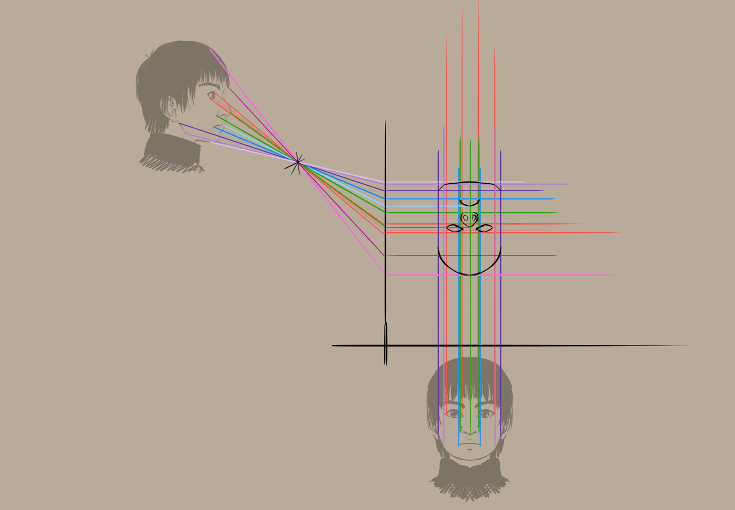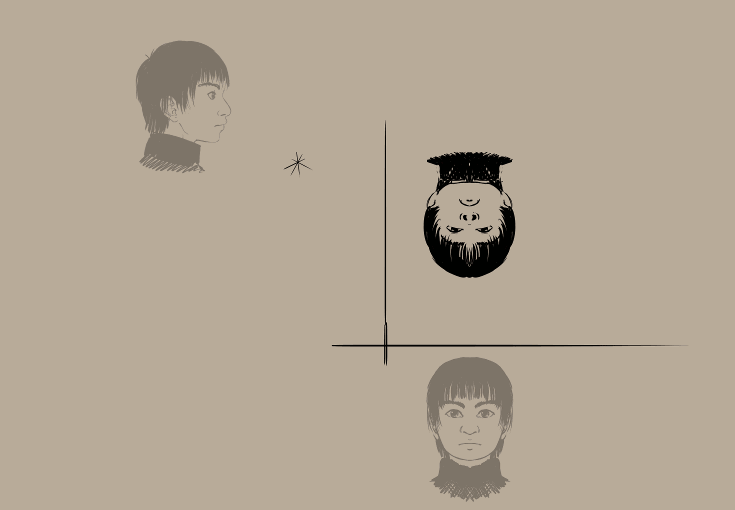
Resultaat:

Ziet er nogal eng uit, he?

En opnieuw is er een eenvoudiger methode om dit te doen…

Wist u u dat u Krita in 3d kunt roteren? Nee?

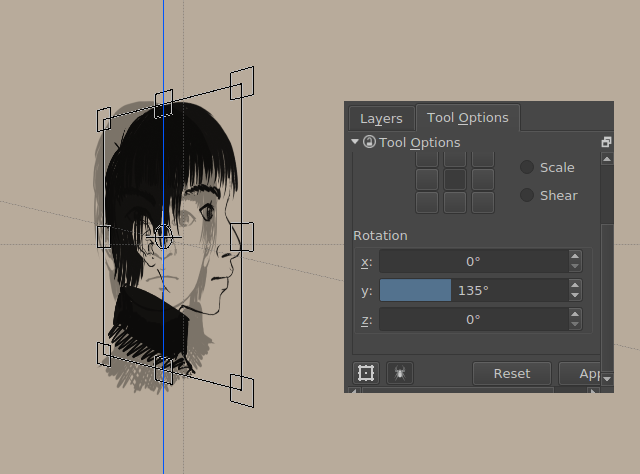
Wel, nu weet u het.

De orthografische vlakken stellen we respectievelijk in op 45 en 135 graden.

Bij het origineel trekken we horizontale lijnen waarvan we lijnen kunnen trekken naar de verdwijnpunten.

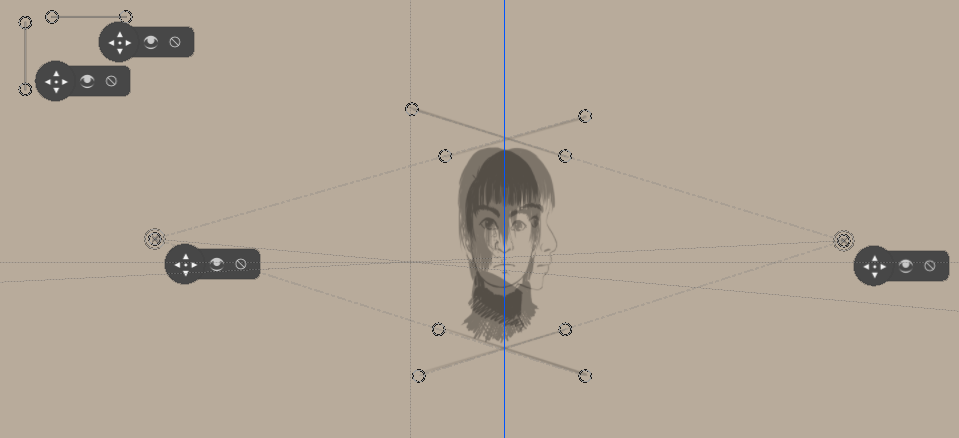
En vanaf hier gaan we net zoals bij de methode met de raaklijnen tekenen. (Vergeet niet de bovenaanzichten!)

Zodat u zoiets als dit zou moeten krijgen:

Maar opnieuw is de normale methode wel een stuk makkelijker…

Maar denkt misschien u: hee, dit is veel werk… Kunnen we het op de een of andere manier met de computer makkelijker maken?

Uhm, ja, dat is min of meer waarom mensen tijd gespendeerd hebben aan het ontwikkelen van grafische 3d technologie:

(De afbeelding hierboven is gemodelleerd in blender met gebruik van onze orthografische referentie)

Laten we daarom in het volgende hoofdstuk bekijken hoe we deze techniek praktisch kunnen gebruiken…