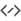Isto é uma continuação do tutorial axonométrico; como tal, certifique-se que o lê antes de ficar confuso!

Projecção em Perspectiva

Deste modo, até agora só temos feito projecções paralelas. Chamam-se assim porque todas as linhas de projecção que foram desenhadas eram paralelas.

Contudo, no mundo real, não temos projecções paralelas. Isto deve-se às lentes nos seus olhos.

As lentes convexas, como esta imagem bonita da Wikipédia mostra-nos que temos a capacidade de transformar raios de luz paralelos em convergentes.

O ponto onde todos os raios se juntam chama-se o ponto focal e o ponto de fuga num desenho 3D relaciona-se com a expressão da distorção máxima que pode ser dada a duas linhas paralelas à medida que se deslocam em direcção ao ponto focal.

Como pode ver na imagem, o ponto focal não é um ponto final dos raios. Em vez disso, é onde os raios se cruzam antes de divergirem de novo… A única diferença é que a imagem resultante será invertida. Mesmo nos nossos olhos, esta inversão acontece, mas os nossos cérebros estão habituados a este fenómeno estranho desde a infância e rodam-no automaticamente.

Vejamos como e possível projectar agora a nossa caixa em perspectiva.

Isto correu relativamente bem. Como poderá ver, reunimos de certa forma os dois lados num só (resultando no quadrado do lado púrpura), pelo que tivemos uma projecção ao longo do tempo mais simples. A projecção está limitada à projecção em um ou dois pontos de fuga, pelo que só as linhas horizontais ficam distorcidas. Também podemos distorcer as linhas verticais

… para obter uma projecção em três pontos, mas isto é um pouco demais. (E cometeu-se um erro aqui…)

Vamos configurar de novo a nossa projecção em perspectiva…

Iremos usar um único ponto de fuga para o nosso ponto focal. Estará lá uma linha-guia para o plano da projecção, onde iremos configurar réguas paralelas horizontais e verticais para desenhar facilmente as linhas rectas desde o plano de visualização até à sua intersecção.

E agora o funcionamento no formato GIF… (não se esqueça que pode rodar a área de desenho com o 4 e o 6)

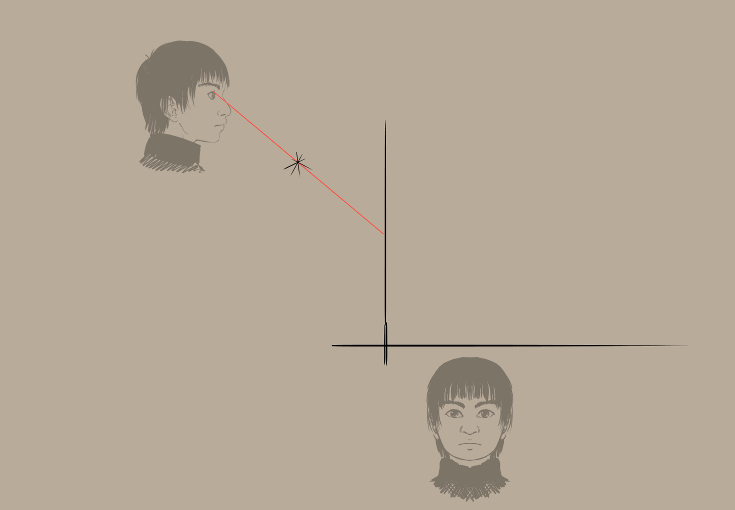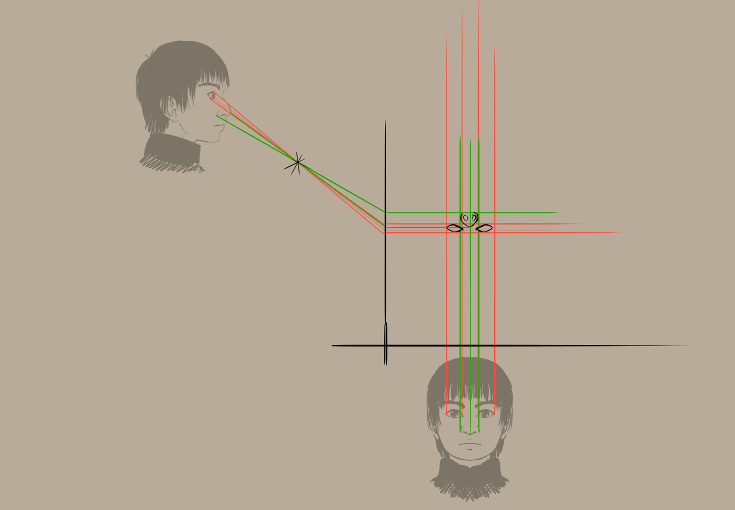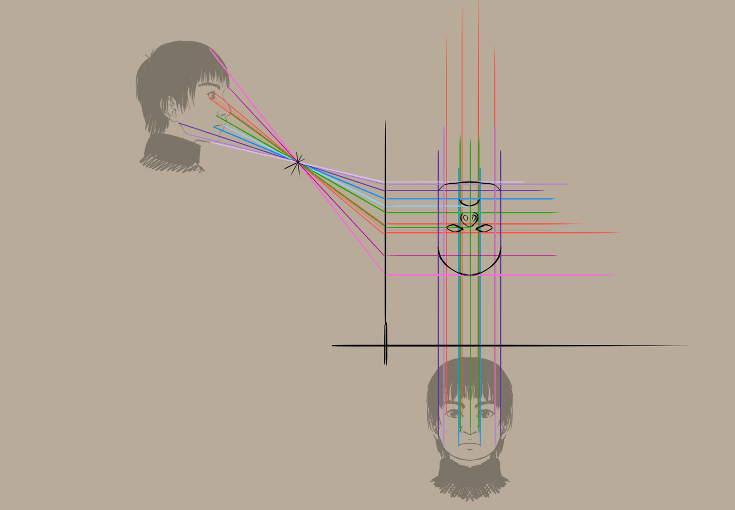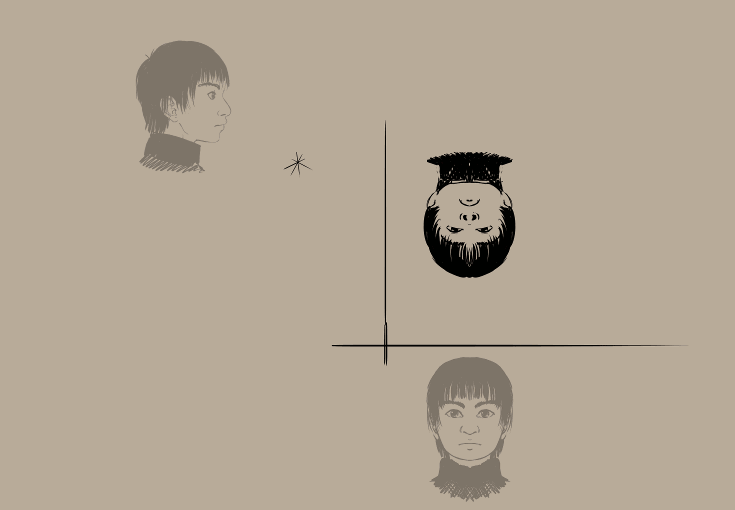
Resultado:

Parece bastante estranho, não parece?

E, mais uma vez, tecnicamente temos aqui uma configuração mais simples…

Sabia que pode usar o Krita para rodar em 3D? Não?

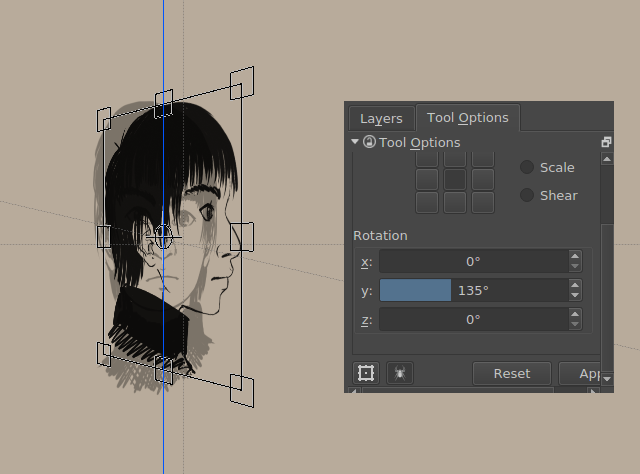
Ok, então agora pode.

Os gráficos ortográficos foram configurados para 45 e 135 graus, respectivamente.

Foram desenhadas linhas horizontais nos originais, para que se possa agora alinhar as réguas do ponto de fuga a elas.

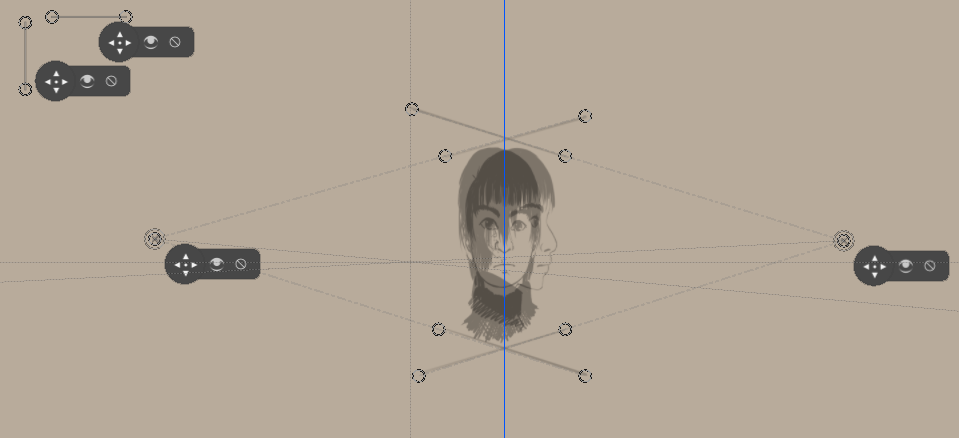
E a partir daqui, como acontece no modo de inclinação, vamos começar a desenhar. (não se esqueça das vistas superiores!)

O que fará com que obtenha algo deste tipo:

Mas, mais uma vez, o método normal é de facto um pouco mais simples…

Mas agora poderá pensar: ena, isto é muito trabalho… Não conseguimos simplificar isto de alguma forma com o computador?

Hum, sim, isto é mais ou menos porque é que as pessoas gastam tempo a desenvolver a tecnologia de gráficos 3D:

(A imagem acima foi esculpida no Blender com a nossa referência ortográfica)

Vejamos então agora como é que esta técnica pode ser usada de forma prática para a parte seguinte…