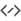Esta é uma continuação do tutorial sobre projecções ortográficas e oblíquas; certifique-se que os consulta se estiver confuso!

Axonométrica

Como tal, a lógica de adicionar o topo é ainda muito semelhante à do lado.

Não é muito interessante. Mas ficará muito mais interessante quando usarmos uma projecção lateral:

Dado que o nosso cubo é vermelho, em ambas as vistas frontais, e azul nos lados esquerdo e direito, podemos simplesmente usar cópias; isto simplifica bastante o método para os cubos. Chamamos a esta forma de projecção axonométrica “dimétrica” porque deforma as duas linhas paralelas de igual forma.

A isométrica é um pouco como a dimétrica, onde temos o mesmo ângulo entre todas as linhas principais:

A isométrica verdadeira é feita com um ângulo 90-54,736=35,264° a partir do plano do chão:

(como pode ver, não se alinha perfeitamente, dado que o Inkscape, embora mais preparado para criar estes tipos de diagramas que o Krita, não tem ferramentas para manipular o ângulo da linha em graus)

Este é um ângulo um pouco estranho e, para além disso, não se alinha sensivelmente com os pixels; por isso, para os jogos de vídeo, é usado um ângulo de 30° a partir do plano do chão.

Muito bem, então agora vamos criar uma isométrica do rapaz.

Iremos criar um novo documento e adicionar uma camada vectorial.

Na camada vectorial, iremos seleccionar a ferramenta da linha recta, iniciar uma linha e depois manter carregado o Shift para que ela se ajuste aos ângulos. Isto irá possibilitar a configuração em 30° como foi feito acima:

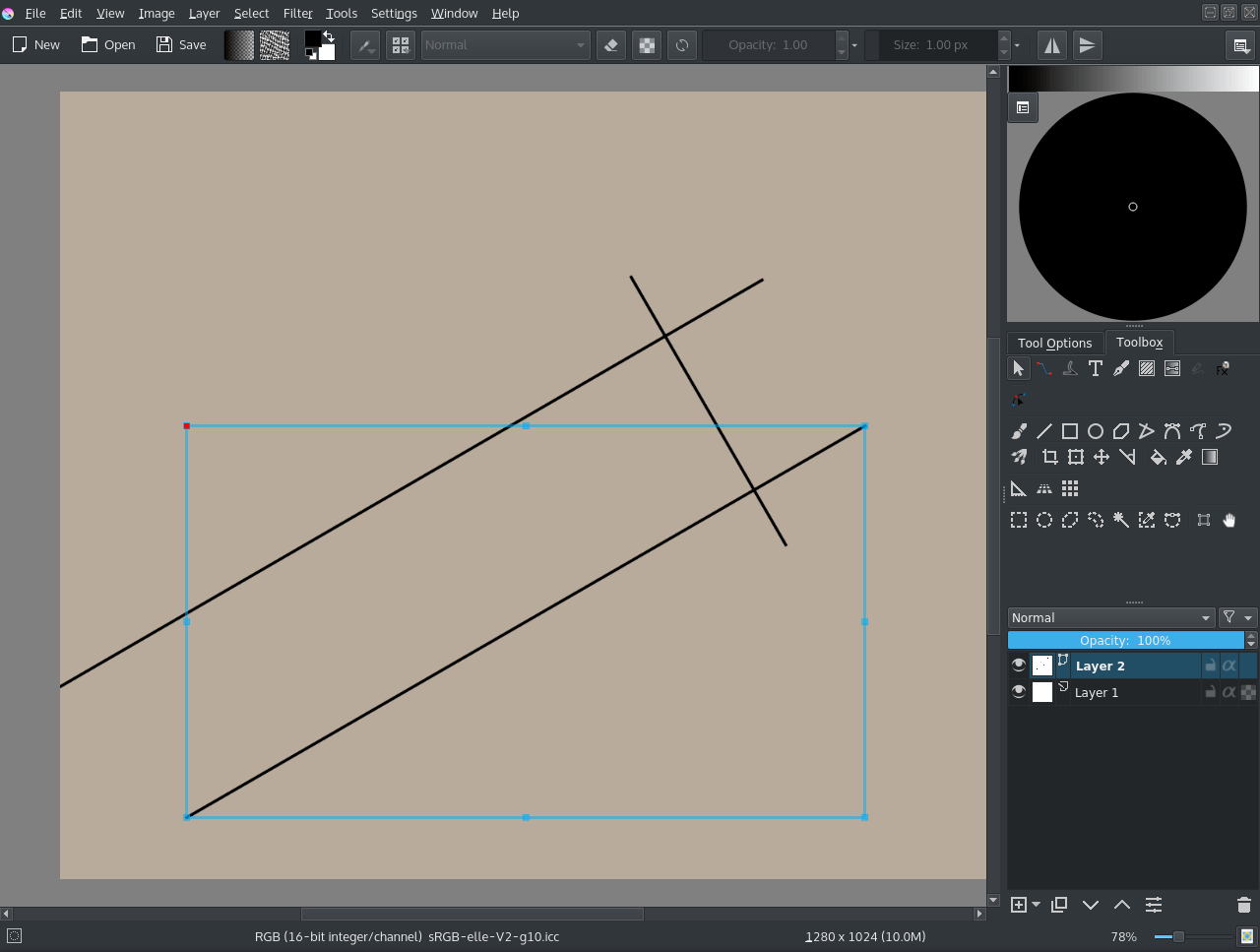
Iremos então importar algumas das imagens da animação através da opção Camadas ‣ Importar/Exportar ‣ Importar uma camada.

Depois iremos recortá-la, seleccionando a ferramenta de recorte como Camada e usando os Filtros ‣ Cores ‣ Cor para o alfa… para remover todo o fundo. Também foi configura a opacidade a 50%. Finalmente, alinham-se os vectores a eles:

Dica

Para dimensionar um vector mas mantendo o seu ângulo, podê-lo-á seleccionar com a ferramenta de tratamento de formas - a seta branca - arraste os cantos da área envolvente para os começar a mover e depois carregue em Shift para restringir as proporções. Isto permitir-lhe-á manter o ângulo.

A imagem inferior é “a parte de trás vista de frente” e será usada para determinar onde irá ficar a orelha.

Agora, obviamente teremos pouco espaço, por isso seleccione a ferramenta de recorte, seleccione a Imagem e assinale a opção Aumentar e depois o seguinte:

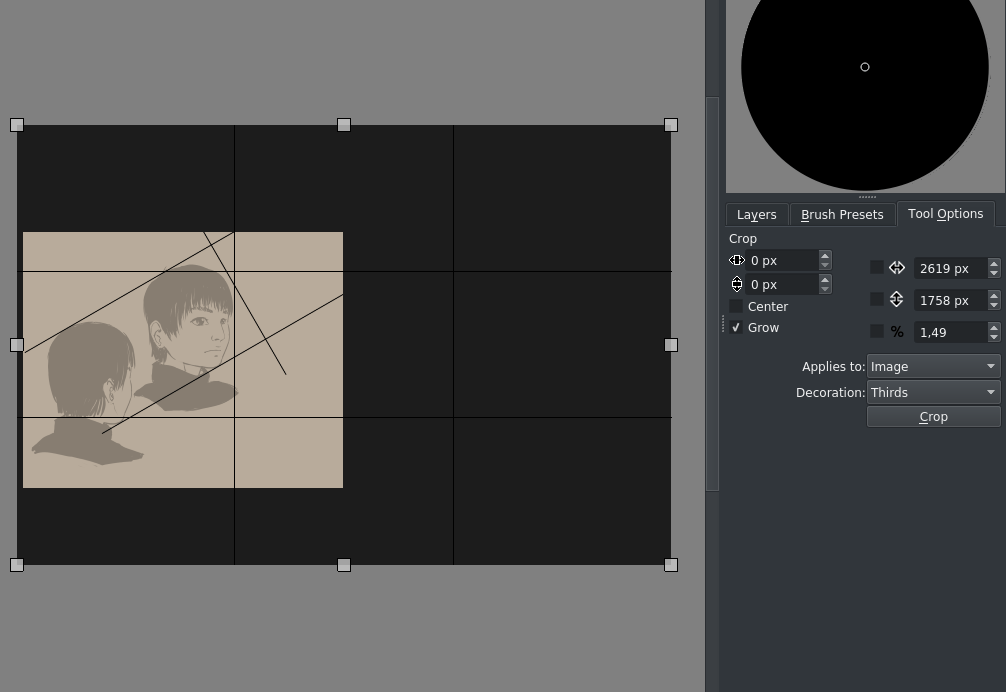
O Aumento é uma forma mais prática de dimensionar imediatamente a área de desenho na sua altura e largura.

Depois iremos alinhar as outras cabeças e transformá-las com as opções da ferramenta de transformação:

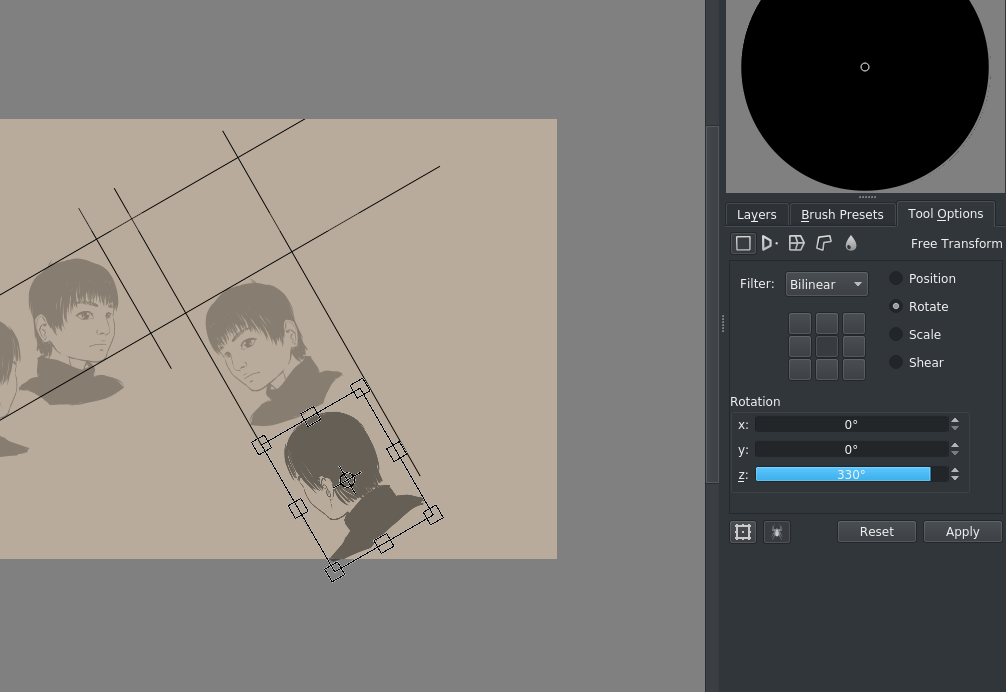
(os 330° aqui são 360°-30°)

O nosso rectângulo que estaremos a tratar lentamente vai ficando visível. Agora, este é um ângulo um pouco difícil de usar, por isso vamos a Imagem ‣ Rodar ‣ Rotação Personalizada e preencher 30° no sentido horário (dos ponteiros do relógio):

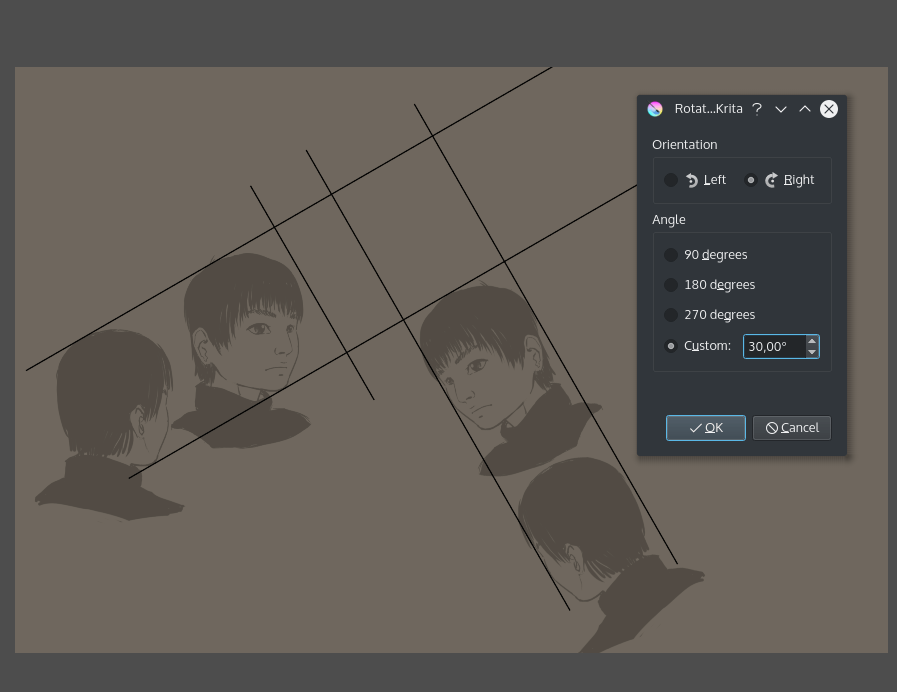
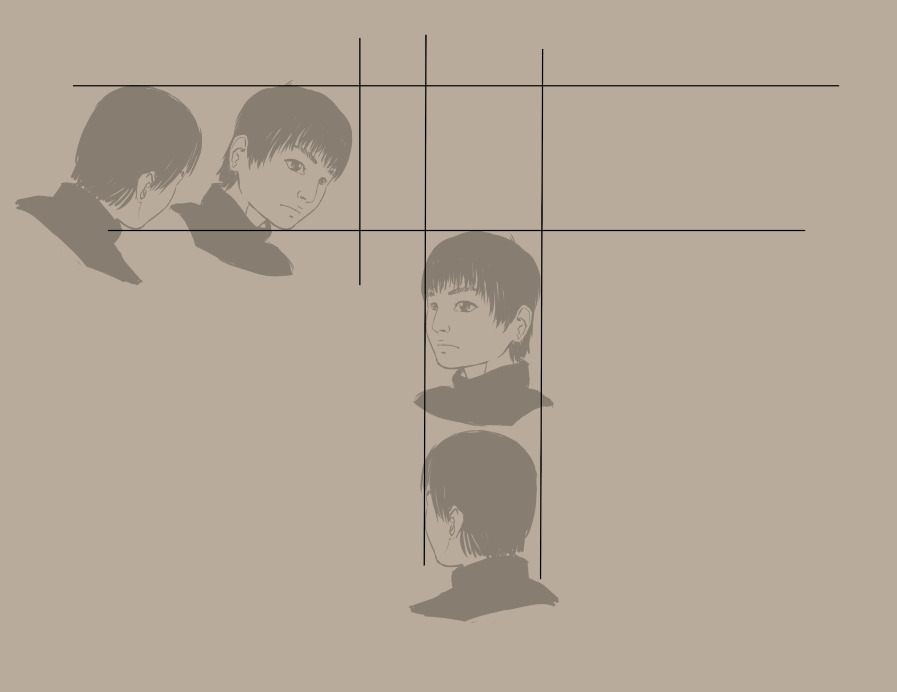
(obviamente poderíamos ter simplesmente rodado as duas imagens da esquerda em 30°; isto é principalmente para ser menos confuso em comparação com o cubo)

Como tal, fizemos alguns recortes, algumas limpezas e adicionámos dois assistentes paralelos como fizemos com a projecção ortográfica:

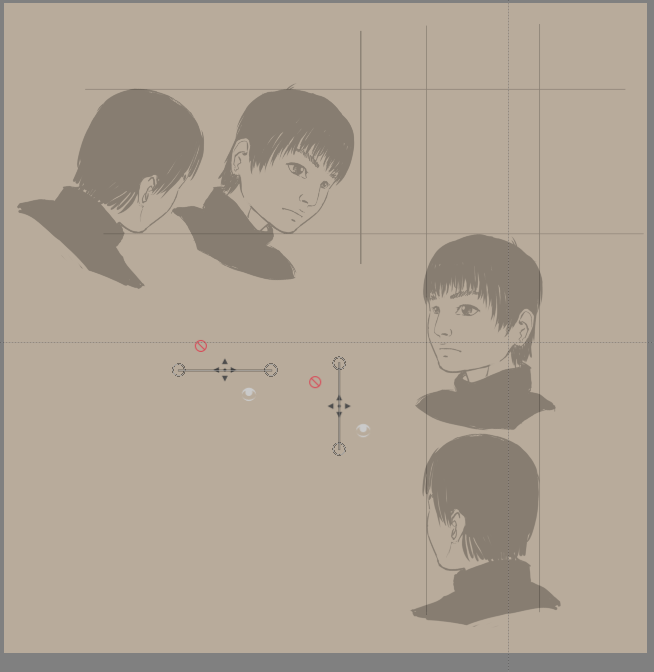
Como tal, a ideia aqui é que desenhe linhas paralelas de ambos os lados para encontrar pontos na área de desenho. Poderá usar as antevisões dos assistentes para manter as coisas arrumadas; contudo, foram desenhadas as linhas à mesma para sua conveniência.

O melhor é criar alguns pontos de amostragem, como as sobrancelhas, e depois desenhar a sobrancelha sobre eles.

Axonométrica alternativa com a ferramenta de transformação

Agora, existe uma forma alternativa de chegar aqui, que não ocupa muito espaço.

Iremos abrir a nossa projecção ortográfica com Abrir um Documento Existente como um Documento sem Título para não gravemos sobre ela.

A nossa isométrica adequada para jogos tem o seu ângulo em dois pixels horizontais e um vertical. Como tal, iremos inclinar as imagens ortográficas com máscaras de transformação iguais a -0,5/+0,5 pixels (isto é proporcional)

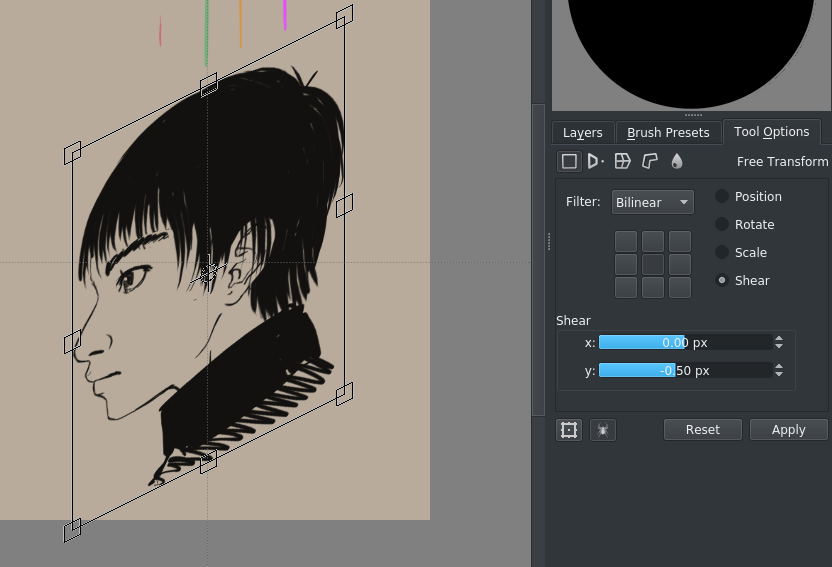
Use a grelha para configurar duas réguas paralelas que representam ambas as diagonais (podê-las-á ajustar com a combinação Shift + S):

Adicione também a vista de topo:

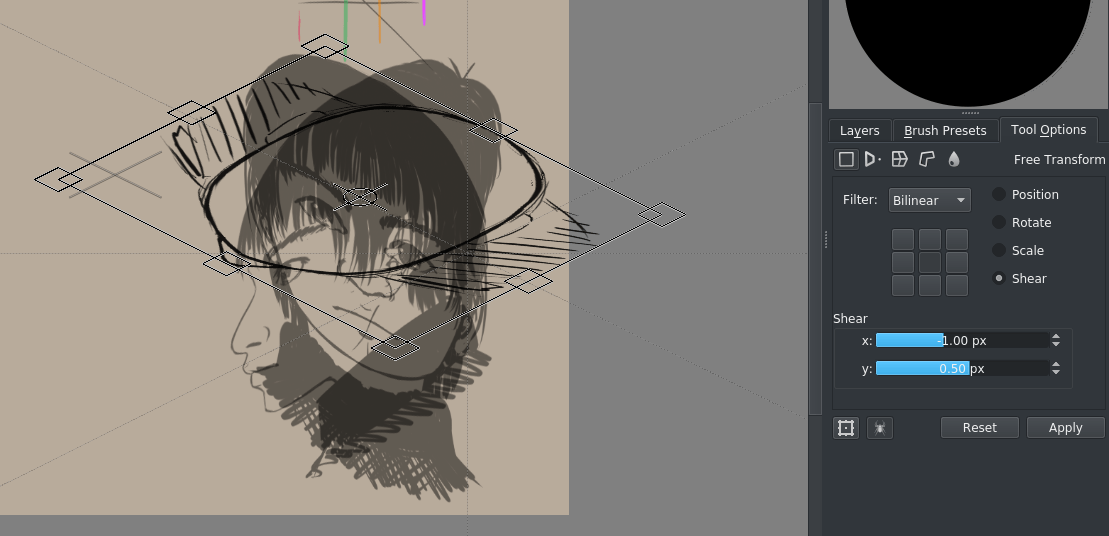
se o fizer para todas as fatias, irá obter algo do género:

Usando as réguas paralelas, poderá descobrir a posição de um dado ponto num espaço 3D:

Como poderá ver, esta versão parece-me mais com uma versão 3D, assim como mais assustadora também.

Isto acontece porque existe menos passos envolvidos que na versão anterior – iremos derivar a nossa imagem directamente da vista ortográfica – como tal, existem menos erros envolvidos.

O susto é derivado de termos aplicado algum estilo na nossa vista lateral, pelo que os olhos agora saem ENORMES. Isto acontece porque, quando estilizamos a vista lateral de um dado olho, tendemos a desenhá-lo não de forma perfeita de um dado lado, mas sim a partir de um dado ângulo. Se olhar com cuidado para a vista rotativa, o mesmo problema acontece aqui também.

De um modo geral, as coisas estilizadas tendem a ficar horríveis numa vista 3D, pelo que poderá ter de fazer algumas escolhas sobre como pô-las a funcionar.

Por exemplo, poderá simplesmente corrigir a vista lateral (como usámos máscaras de transformação, isto é simples.)

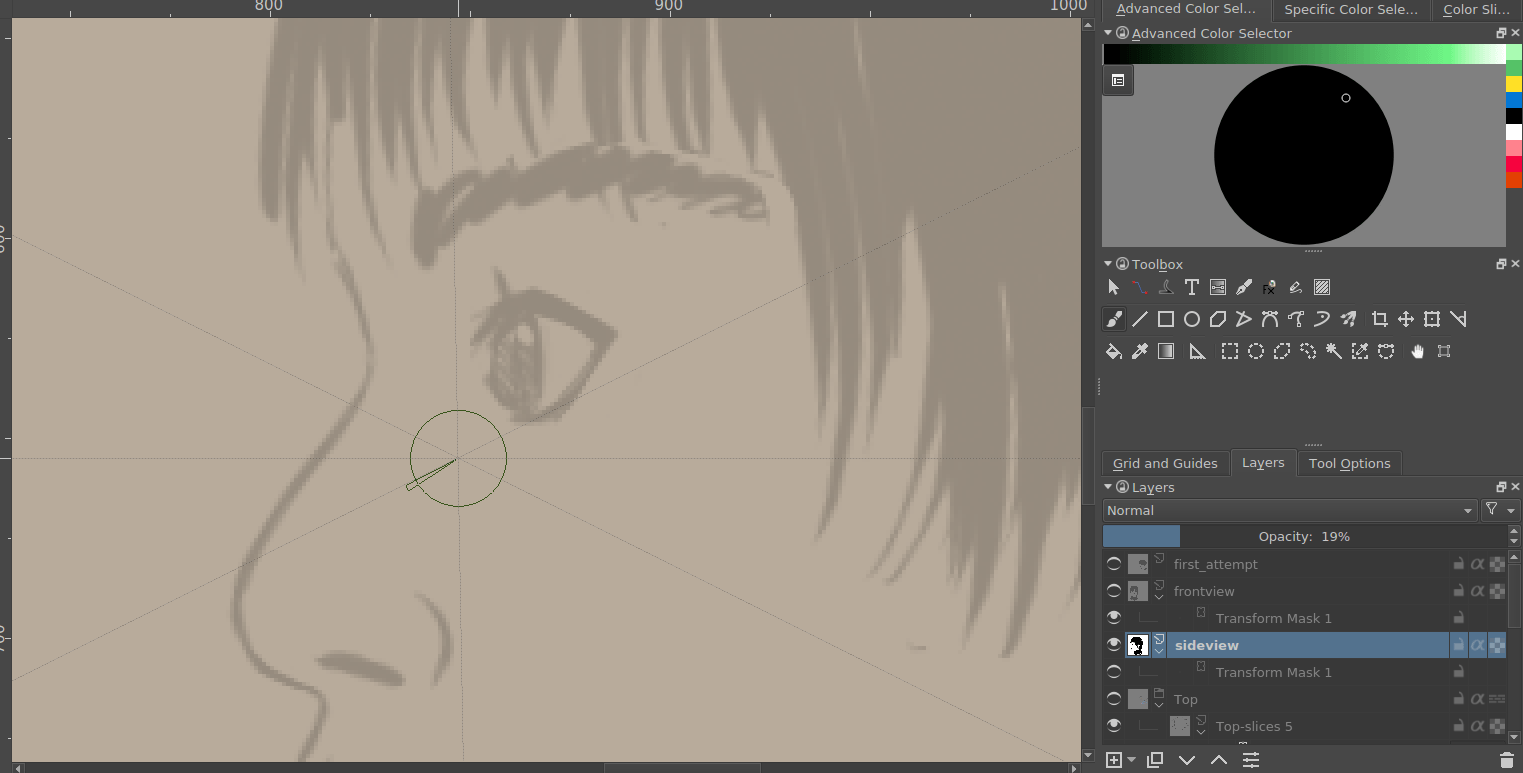
E depois gerar um novo desenho a partir daí…

Compare com o antigo e poderá ver que os olhos do novo resultado parecem muito menos assustadores:

Ainda parece um pouco esmagado em comparação com a projecção paralela normal acima, e poderá ser uma ideia não apenas inclinar, mas também esticar um pouco os pontos.

Iremos continuar com a projecção em perspectiva no próximo!