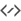Aquesta és una continuació de la guia d'aprenentatge de la projecció axonomètrica, assegureu-vos de comprovar-la si us confoneu!

Projecció en perspectiva

Així doncs, fins ara només hem fet projecció en paral·lel. S'anomena així perquè totes les línies de la projecció que hem dibuixat estan paral·leles.

No obstant això, en la vida real no tenim una projecció en paral·lel. Això es deu a la lent en els nostres ulls.

Les lents convexes, tal com ens mostra aquesta bella imatge de la Viquipèdia, tenen la capacitat de convertir els raigs de llum paral·lels en convergents.

El punt on s'uneixen tots els raigs s'anomena punt focal, i el punt de fuga en un dibuix en 2D està relacionat amb aquest, ja que és l'expressió de la distorsió màxima que es pot donar a dues línies paral·leles a mesura que s'inclinen cap al punt focal.

Com podeu veure a la imatge, el punt focal no és el punt final dels raigs. Més aviat, és on es creuen els raigs abans de divergir novament… L'única diferència és que la imatge resultant s'invertirà. Aquesta inversió succeeix fins i tot amb els nostres ulls, però el nostre cervell està acostumat a aquest desgavell des de la infància i li donarà la volta de manera automàtica.

Vegem si ara podem projectar en perspectiva el nostre quadre.

Això va força bé. Com podeu veure, hem de fusionar els dos costats en un (el qual resultarà en el costat porpra del quadrat) perquè sigui més fàcil a l'hora de projectar. La projecció està limitada a una o dues projeccions del tipus punt de fuga, de manera que només es distorsionen les línies horitzontals. També podem distorsionar les línies verticals

…per a obtenir una projecció de tres punts, però això és una mica massa. (I aquí m'he equivocat totalment…)

Configurarem la nostra projecció en perspectiva de nou…

Utilitzarem un únic punt de fuga per al nostre punt focal. Hi haurà una línia guia per al pla de la projecció, i establirem regles paral·lels horitzontals i verticals per a dibuixar amb facilitat les línies rectes des del pla de visió fins al punt d'intersecció.

I ara el flux de treball per al format GIF… (recordeu que es pot girar el llenç amb les tecles 4 i 6).

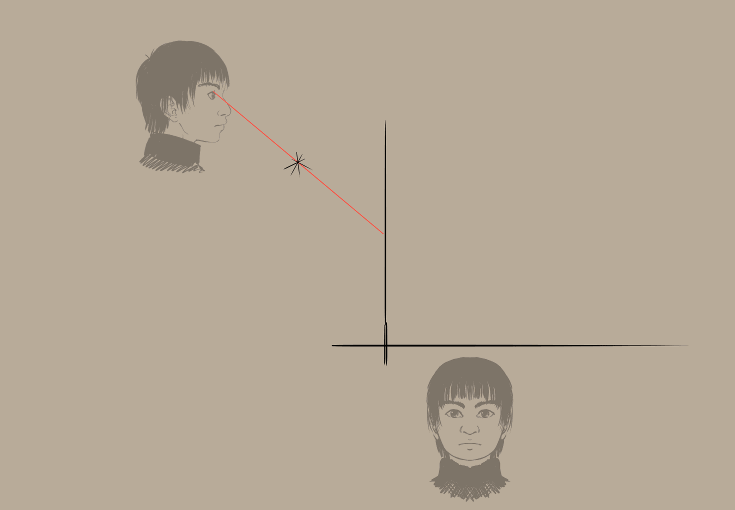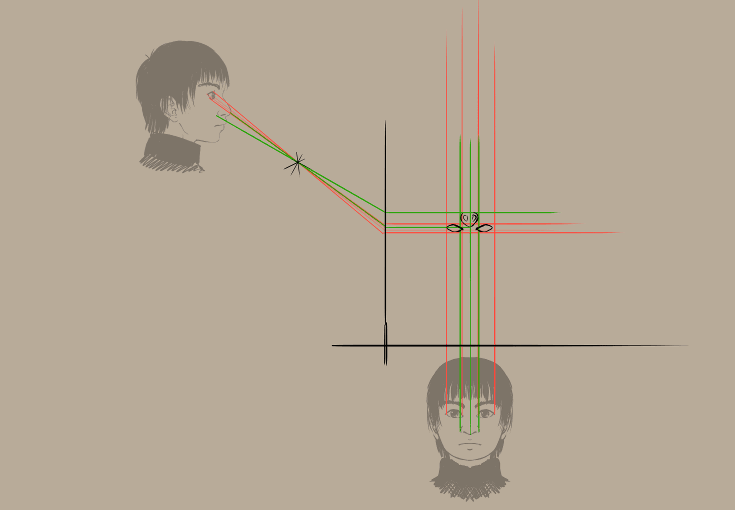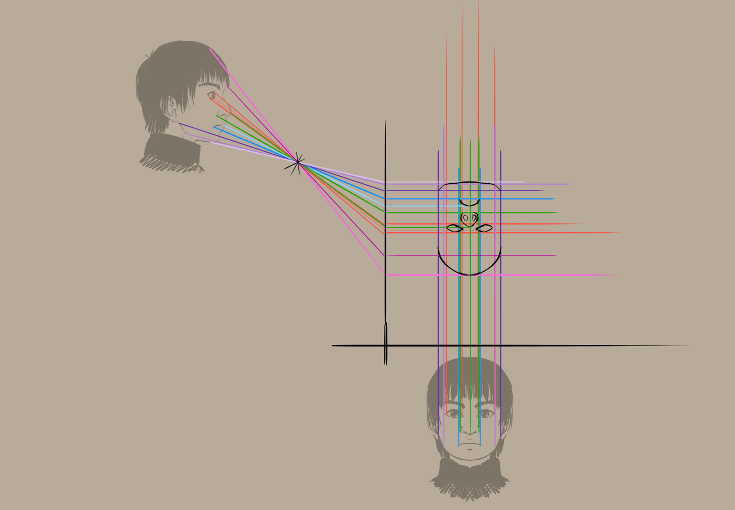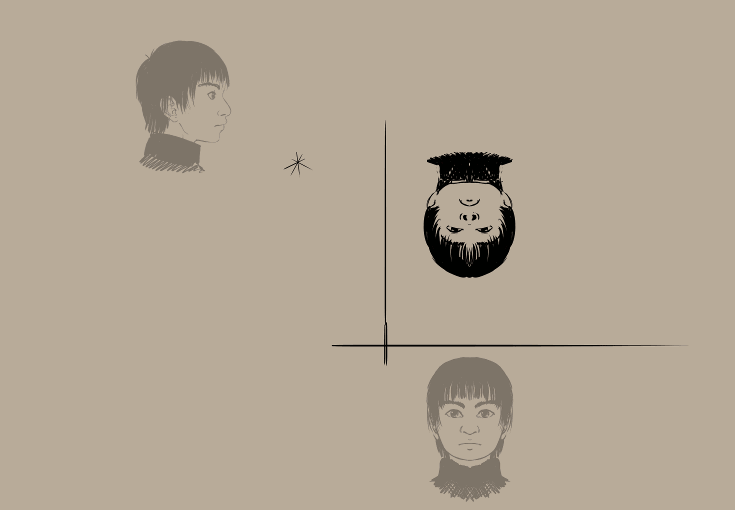
Resultat:

Sembla molt arrogant, no?

I de nou, tècnicament hi ha una configuració més senzilla…

Sabíeu que podeu utilitzar el Krita per a girar en 3D? No?

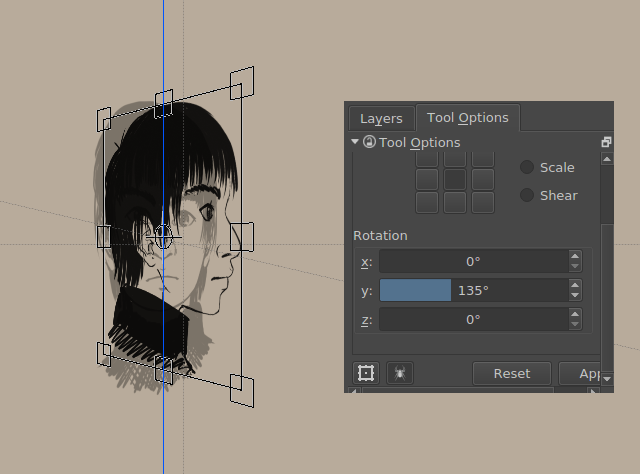
Bé, ara sí.

Els gràfics ortogràfics s'han establert a 45 i 135 graus respectivament.

Dibuixem línies horitzontals sobre els originals, de manera que puguem alinear-les amb els regles dels punts de fuga.

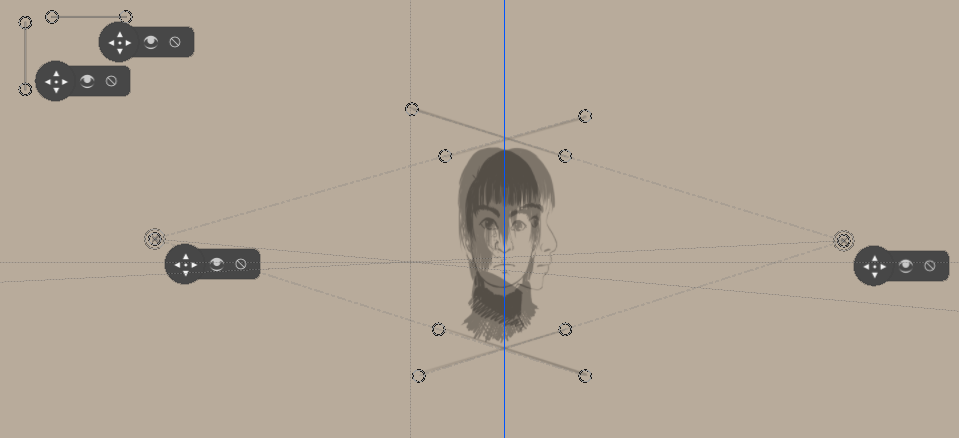
I a partir d'aquí, com amb el mètode d'inclinar, comencem a dibuixar. (No oblideu les vistes superiors!)

El que hauria de donar-vos quelcom com això:

Però novament, el mètode habitual és en realitat una mica més fàcil...

Però ara podríeu estar pensant: Caram! Això és molta feina… No podem facilitar-ho d'alguna manera amb l'ordinador?

Per descomptat, aquí és més o menys on passa el temps la gent que desenvolupa tecnologia de gràfics en 3D:

(La imatge de dalt està esculpida en Blender emprant la nostra referència ortogràfica).

Així que vegem una aplicació pràctica d'aquesta tècnica en la següent part...